Chapter 1: Introduction to Topological Wonders

Topology is a fascinating field of mathematics that allows us to visualize complex concepts in ways we never thought possible. Quotient spaces, fiber bundles, and coverings provide us with both simple and profound examples that enhance our mathematical imagination.

A Klein Bottle serves as an intriguing example derived from a specific quotient map applied to a rectangle. By twisting the identification of opposite sides of a paper strip, we create a flat Möbius strip, a non-orientable surface that retains its Euclidean properties. Further identification through self-suturing of the remaining edge of the Möbius strip leads to the formation of the Klein Bottle. The interactions between Möbius strips and Klein bottles can be quite playful. For instance, a Möbius strip can transform into a Klein bottle that then divides into two Möbius strips. Conversely, if we reverse the process, we can visualize two Möbius strips joining to create a Klein bottle, which subsequently splits into two.

This exploration is dedicated to Bella L, whose insightful article on tacos provides a delightful entry point into these concepts.

Section 1.2: Understanding Quotient Spaces

In topology, a quotient map identifies sets of points within a topological space as equivalent, effectively "gluing" them together. For instance, two edges of a rectangle can be identified to form a cylinder. Watching videos that illustrate these identifications can greatly enhance our understanding of two-dimensional manifolds. For example, a quotient map that identifies all points on the edge of a disk can yield a sphere, a concept that can be visualized through practical examples.

For a more thorough exploration of these topics, consider reading Chapter 7, "Surfaces By Identification," in Bert Mendelson's "Introduction to Topology." While there are more rigorous texts available, Mendelson's work provides an accessible starting point for those new to the field.

Chapter 2: The Taco Division Problem

This problem leads us to a generalized version through recursive quotient maps and identifications of equal sectors of a paper disk. Each fold doubles the number of sectors, and through a series of folds, we can visualize how the disk is transformed.

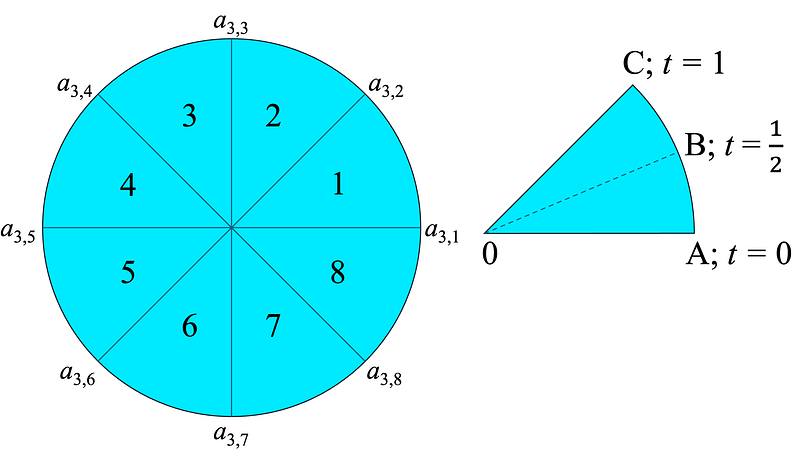
As we identify the copies in the cover and cut the sector in half, we arrive at a network of points within the original disk that are mapped to specific locations, effectively dividing the disk into eight distinct sectors.

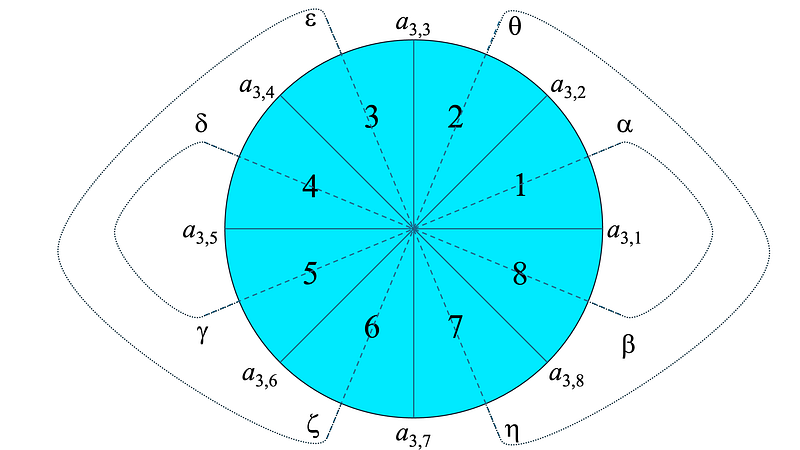
Thus, the entire disk can be conceptualized as a covering space or a fiber bundle, where multiple copies of a sector “hover” above the base sector.

Section 2.1: Exploring Fiber Bundles

Fiber bundles extend our understanding of topological spaces by providing a framework that looks locally like a Cartesian product but can possess more complex global structures.

The fascinating concept of the Hopf fibration, a specific topology of unit quaternions, deserves its own exploration.

Chapter 3: The World of Surfaces by Identification

Two well-known examples of flat (Euclidean) quotient spaces are the Möbius strip and the Klein bottle. Both begin with a rectangle but differ fundamentally in how their edges are identified.

These two surfaces, along with the familiar plane, cylinder, and torus, represent all possible geodesically complete two-dimensional smooth, flat manifolds.

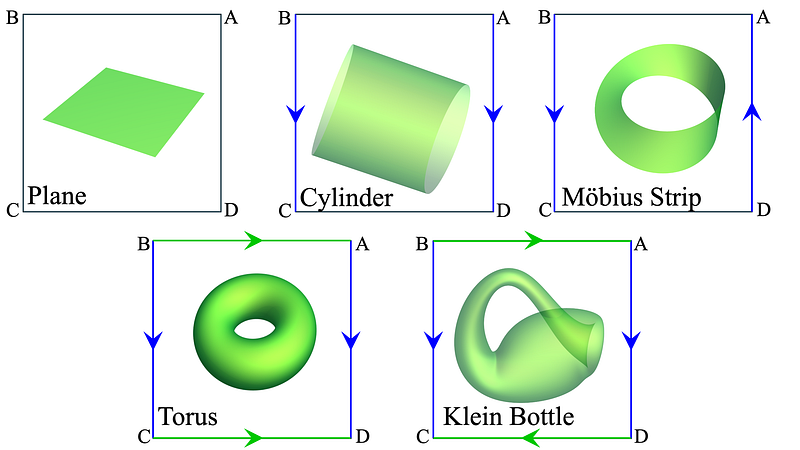
Ultimately, the Klein bottle and torus are the only compact, flat, geodesically complete two-dimensional manifolds. Their unique properties lead to intriguing discussions about how they can be embedded within higher dimensions without self-intersection.

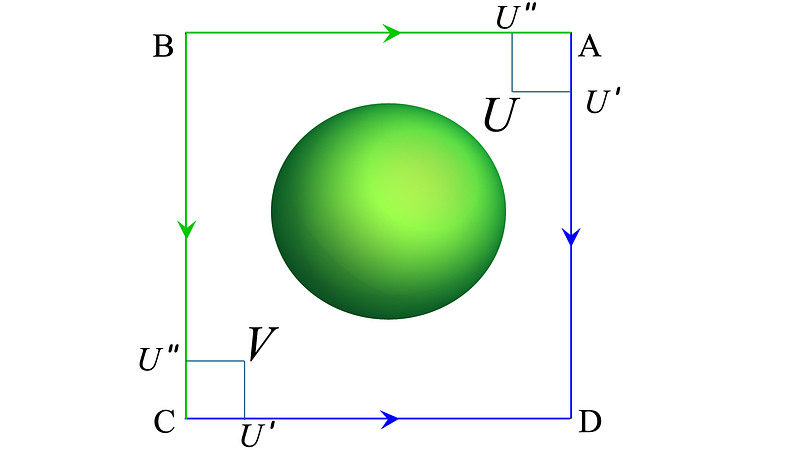
These explorations not only enrich our understanding of topology but also reveal the beauty and complexity of mathematical structures.