Understanding the Rendezvous Challenge in Multi-Agent Systems
Written on
Chapter 1: Introduction to Networked Control Systems
In a prior article, I provided an overview of networked control systems, highlighting how various academic disciplines, particularly graph theory, contribute to the modeling of multi-agent systems.
Section 1.1: Defining the Rendezvous Problem
This article focuses on a core issue within the domain of networked control systems, known as the Rendezvous Problem.
What exactly is the Rendezvous Problem?
The scenario involves N robots, each starting from different locations:
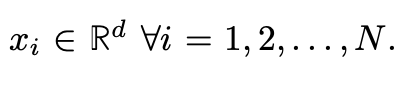
In a two-dimensional environment, we denote this as d=2. Conversely, for aerial or three-dimensional contexts, d becomes 3. The objective is to coordinate all robots to converge at a specific location using a well-defined control strategy. The movement dynamics for each agent i is represented as follows:
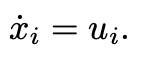
Here, the subscript i indicates an arbitrary agent from the total N agents. Solving this problem involves figuring out how to choose the control law ( u_i ) so that all agents can successfully rendezvous at a designated point, referred to as ( x_M ).

Section 1.2: Practical Constraints of the Rendezvous Problem
There are several real-world challenges associated with this problem. Notably, two constraints are the absence of GPS and the limited sensory range of the robots. Due to the lack of GPS, robots lack knowledge of absolute positions. Furthermore, due to their limited range of perception, robots i and j can only detect each other if they are within a certain distance, denoted as delta:
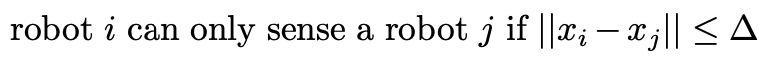
Given that robots typically do not possess information about the absolute coordinates of their peers, they rely on relative distances, which can only be gauged if within a defined delta based on their sensory capabilities. Thus, agents i and j can determine a range of relative distances:
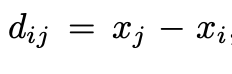
Chapter 2: Path to a Solution
While the problem setup has been laid out, the means to achieve a solution—how to direct each agent to reach a common destination—has yet to be explained. In the next article, I will simplify the scenario by focusing on just two agents and provide a solution to the rendezvous challenge in this context. Additionally, I plan to demonstrate a simulation through code that verifies the efficacy of the control law, showing that the point masses do indeed converge.
Until next time,
Caleb.
The first video titled "Stanford Seminar - Why would we want a multi-agent system unstable" discusses the implications and considerations of multi-agent systems in unstable environments.
The second video, "Multipoint Rendezvous and Multigroup Cooperative Herding," explores strategies for achieving cooperation among multiple agents in various settings.