Chapter 1: Introduction to the Problem

In the realm of number theory, the quest for x and y is a classic challenge. Such problems not only have historical significance but also find applications in contemporary fields like cryptography. Various methods exist to tackle this problem, but one particularly efficient approach stands out, especially when dealing with larger numbers. Let’s explore this classic conundrum together, and don’t forget to check the solution provided below!

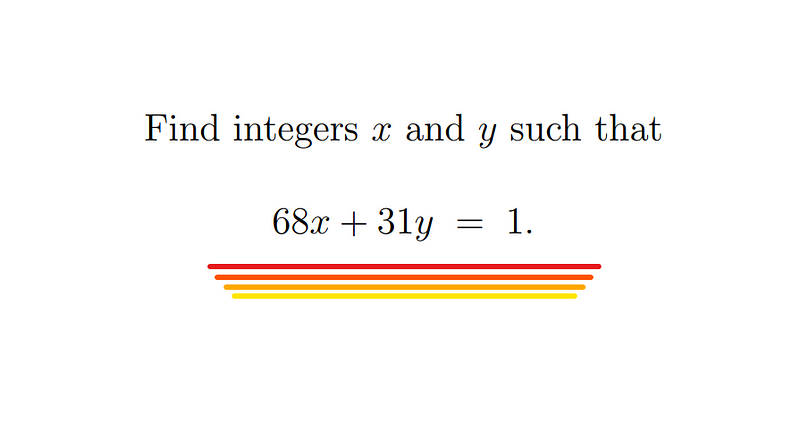
Chapter 2: Establishing the Existence of x and y

To determine the values of x and y, we must first establish that such integers can be found. Bézout’s lemma is a key theorem in mathematics that applies here:

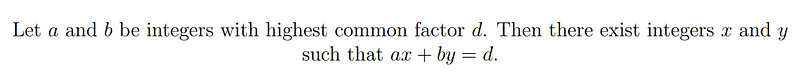
According to Bézout’s lemma, integers x and y exist for the equation 68x + 31y = 1 if the highest common factor (HCF) of 68 and 31 is 1. Indeed, the HCF of these two numbers is 1, but we will need to perform some calculations to find the specific values of x and y.

To do so, we will employ the Euclidean algorithm, which utilizes the process of repeated division with remainders. Let’s start by dividing 68 by 31:

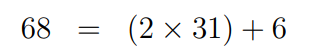
Next, we take the last two results: 31 and 6, and continue the process:

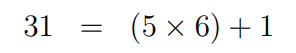
Now, we work with 6 and 1. We repeat the division until we find there’s no remainder:

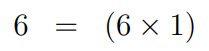
At this point, we see that the process is complete, confirming the HCF of 68 and 31 is indeed 1. This means we can proceed to find x and y. We’ll backtrack through our calculations to express 1 as a combination of 68 and 31. Let’s start by rearranging one of our earlier equations from dividing 31 by 6.

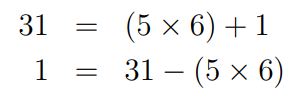
From our earlier division of 68 by 31, where the remainder was 6, we can rearrange as follows:

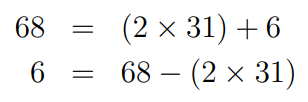
Now that we have 6 as a linear combination of 68 and 31, we can substitute this back into our earlier rearrangement and expand:

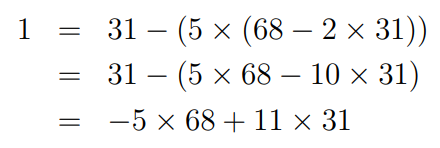
This final equation leads us to the solution:

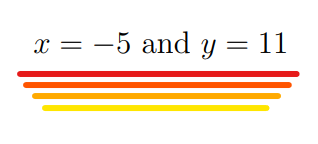
And there we have it! The problem is resolved, revealing a pair of integers. Notably, there are infinitely many solutions, but we’ve found a neat representation in this case.

Challenge 1: Is it possible to find integers x and y such that 42x + 87y = 1?

Challenge 2: Can you determine integers x and y such that 233x + 88y = 1?

Chapter 3: Engaging with Visual Learning

To enhance your understanding of these concepts, consider watching the following videos.

The first video titled "Can You Find Angle X? | Geometry Challenge!" presents a fun and engaging way to apply these mathematical principles.

The second video, "Solve for x in One Step (Simplifying Math)," provides straightforward techniques for solving equations effectively.