Chapter 1: Introduction to SO(3)

The collection of transformations that maintain length and orientation in three-dimensional space is referred to as SO(3). Here, 'S' signifies 'special', and 'O' denotes 'orthogonal'. A special transformation retains orientation while excluding reflections, and an orthogonal transformation preserves lengths. Together, these transformations constitute a mathematical 'group'. A key feature of a mathematical group is its closure property; when combining transformations of this nature, the outcome remains within the set of transformations that uphold length and orientation. Additionally, this group possesses inverses and an identity element.

To illustrate, consider a three-dimensional vector of constant length attached to a fixed point in space. Visualize rotating it around like a loose rod pivoted at one end, moving through various angles. This transformation is part of SO(3) as it maintains the vector's length and orientation. These transformations can be represented using matrices. In three dimensions, this involves a 3x3 matrix applied to a three-dimensional vector, while in two dimensions, a 2x2 matrix is used for a two-dimensional vector.

Section 1.1: Geometric Insight into SO(3)

Before delving into the mathematical representation of three-dimensional rotations, let's gain some geometric understanding. The first step involves selecting an axis of rotation. In three-dimensional space, numerous axes can be chosen, which we can visualize on a unit sphere. The rotation axis is merely a directional vector, and since the length of this vector is unimportant, we can represent it as a unit vector on the two-sphere, denoted as n ? S².

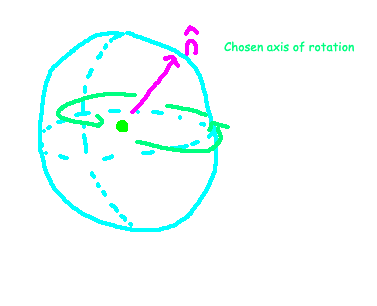
In the illustration above, the pink line labeled n indicates our chosen rotation axis, confined to a unit sphere for simplicity. The circular arrows around this axis depict the rotation process. The next step is to establish the angle of rotation. Initially, we might consider rotating within an angle range of ? ? [0, 2?), but upon further reflection, it becomes evident that this leads to double-counting. Specifying a rotation solely by the axis n and angle ? ? [0, 2?) provides redundant information. For instance, rotating about axis n by an angle of ? = ?/2 is equivalent to rotating about the -n axis by ? = 3?/2. Thus, we can refine our angle range to [0, ?), which is sufficient for parameterizing SO(3).

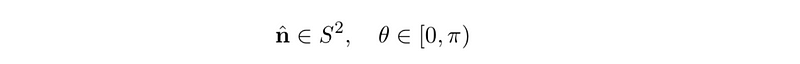
Section 1.2: Matrix Representation of SO(3)

Next, we will explore how to represent elements of SO(3) using matrices. First, we determine the eigenvalues of these matrices. Matrices serve as transformations, and their eigenvalues reflect the scaling characteristics of these transformations. Given that the elements of matrices in SO(3) are real, their characteristic polynomial must also have real coefficients, leading us to expect one real eigenvalue and two complex eigenvalues. Consequently, the eigenvalues are expressed as 1, e^(i?), e^(-i?).

Consider n as a unit modulus eigenvector of M ? SO(3), where Mn = n. A rotation about this axis can be expressed mathematically as:

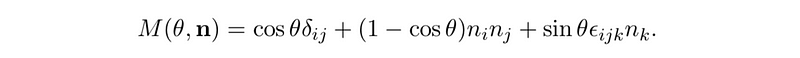
Here, theta indicates the angle of rotation. The mathematical expression can be complex, but it is important to note that it provides the matrix element located in the ith row and jth column. The vector n acts as the axis of rotation because it remains unchanged under the transformation. However, ambiguities arise in this description; for example, mapping ? ? 2? ? ? yields the same result as mapping n ? -n. Additionally, a rotation by 0 degrees results in no change, thus introducing further redundancy in our system.

Chapter 2: Exploring the Topological Nature of Rotations

The first video titled "Group of Rotations" provides a deeper understanding of how rotation groups function mathematically and geometrically, illustrating various transformations.

We can approach the geometry of our rotation group from a different perspective. Rather than viewing it as points on a sphere, we can think of it as points within a ball. We can create a new mapping from our original manifold—a hollow sphere—to a solid ball. Given that we have determined the need for both an axis of rotation and an angle, we can combine these aspects to express any rotation as a vector of variable length.

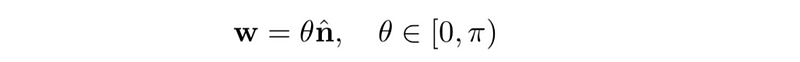
This aligns with our previous identification, as when ? = 0, w = 0 serves as the identity element. To maintain consistency with earlier findings, we can define the ball with a radius ?.

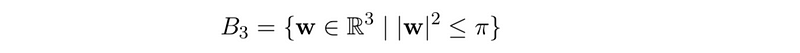
However, due to our earlier identification condition, antipodal points on the boundary sphere are treated as equivalent. Thus, the boundary of this manifold is represented as ?B³/ ?, where our equivalence relation identifies these antipodal points. This indicates that our manifold lacks a boundary, as points on the boundary sphere are not unique. While this manifold is connected, it is not simply connected. A straight line through the origin would form a loop since antipodal points are identified, preventing contraction. However, it is possible to construct a loop entirely within the interior of the sphere.

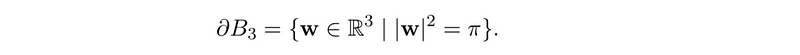
Interestingly, we can "square" a loop by traversing directly through the sphere twice, resulting in a curve that can be deformed to a point. The homotopy group of a mathematical structure describes how many loops must be wrapped around before shrinking it to a point. For a sphere, the homotopy group is trivial, meaning any loop can be reduced to a point. In contrast, for our structure, we require two wraps, suggesting that the homotopy group resembles Z².

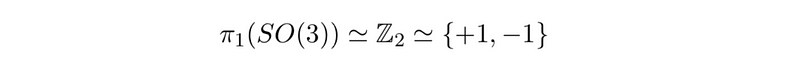
The group Z² represents a cycle group consisting of two elements. This manifold is compact because it is bounded and closed, including points on its boundary.

The second video titled "Determining Which of a Group of Shapes Has Rotational Symmetry" explores the principles of rotational symmetry, providing visual examples and explanations of this concept in various shapes.