Understanding the Higgs Mechanism: A Clear Explanation
Written on
Chapter 1: The Essence of the Higgs Mechanism
For those with a basic grasp of physics, the metaphorical descriptions surrounding the Higgs boson’s role in “imparting mass to other particles” can often be unsatisfactory. Unlike gravity and electromagnetism, which are elucidated through precise mathematical equations that yield measurable results, the explanation of the Higgs boson is less straightforward.

A recent analysis by Ethan Siegel highlights that the majority of the Universe's mass originates from strong interactions within nucleons (protons and neutrons). This means that the mass ( m ) of a proton is primarily a consequence of the interactions among its constituent particles, where their combined energy correlates to ( mc^2 ).
However, the rationale behind the belief that the “Higgs boson imparts mass to fundamental particles” isn’t immediately evident. I have authored several scientific papers on this topic, which I will summarize here. A fundamental understanding of electromagnetic fields is assumed for further reading.
Consider a charged particle at rest within a uniform electric field ( E ), similar to what you might find between the plates of a parallel plate capacitor. The voltage at a distance ( h ) from one of the plates is described by ( V = Eh ), where ( V ) signifies the potential at that point.
The particle’s energy can be expressed as ( U' = qV ), where ( q ) is the coupling constant between the particle and the field ( E ). This energy serves as an indicator of the interaction strength between the particle and the field. Generally, potential energy is represented as ( U' = cP ), with ( c ) being a coupling constant and ( P ) a scalar function dependent on the fields and coordinates.
The energy contained within the volume ( Sd ) of the capacitor—where ( S ) is the plate area and ( d ) is the distance between them—is carried by the electric field, given by ( u = frac{1}{2} epsilon E^2 Sd ). Notably, the energy held by a field is proportional to its strength squared, as illustrated by the magnetic energy density in a solenoid, ( u = frac{B^2}{2mu} ). Thus, the total energy in the capacitor region can be expressed as ( U = U' + u = qV + frac{1}{2} epsilon E^2 Sd ).
According to Einstein, we must also consider the rest energy of the charged particle, whose mass is ( m ). This modifies ( U ) to ( U = qV + frac{1}{2} epsilon E^2 Sd + mc^2 ). Where does this last term originate? It doesn’t fit the forms of ( cP ) or ( epsilon F^2 )!
To clarify, let’s introduce another field ( W' ) with potential ( H' ) that the particle also interacts with, characterized by a coupling constant ( g ). Consequently, the total energy can be expressed as ( U = cP + frac{1}{2} epsilon E^2 Sd + gH' + frac{1}{2} epsilon W'^2 Sd ). The ( frac{1}{2} ) factor in the latter term is introduced for clarity in comparisons.
Assuming that unlike ( E ) or ( B ), the ( W' ) field fills the universe such that its minimum value is not zero but ( W_0 ), we can redefine ( W' = W_0 + W ) and correspondingly ( H' = H_0 + H ). The additional field contributes energy to the system, leading to an expanded formulation.
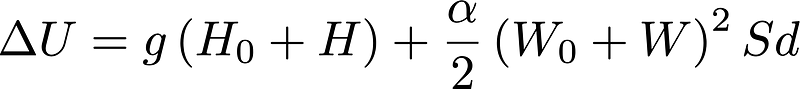
Upon simplification and expansion, we can observe that
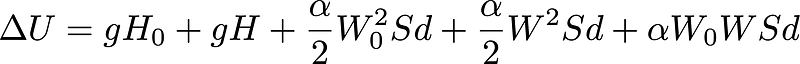
The first term in this expansion is a constant dependent on the coupling between the particle and the Higgs field ( H_0 ). This coupling varies from one particle to another. If ( mc^2 = gH_0 ), the origin of the rest energy becomes apparent: it is a measure of how strongly a (massless) particle interacts with the ubiquitous Higgs field present throughout the universe.
It’s important to note that all other terms can be interpreted to demonstrate the expected behavior of the Higgs field within the standard model: there are interactions between Higgs bosons and matter particles, a mass term for the Higgs field itself, and self-coupling of the Higgs field. For more detailed insights, consider reading one of the papers listed in the bibliography below.
The model clarifies how strong interactions within nucleons result in a mass term. The mechanism is analogous: the strong field, depicted in quantum mechanics by gluons, interacts with quarks over a minuscule volume, resulting in an interaction energy of ( Delta G' = sigma(G_0 + G) ). The “constant” term ( Delta G_0 ), which depends on the interacting particles, manifests as ( mc^2 ), where ( m ) represents the mass of the nucleon (either a proton or a neutron).
- Organtini, "Unveiling the Higgs mechanism to students", Eur. J. Phys. 33 (2012) 1397–1406 (arXiv:1207.2146v2)
- Organtini, "An introduction to the Higgs mechanism based on classical physics secondary school curriculum", PoS EPS-HEP2017 (2017) 563.
- Organtini, "The Higgs mechanism for undergraduate students", Nuclear and Particle Physics Proceedings 273–275:2572–2574.
Chapter 2: Insights from Video Explanations
For a visual breakdown of the Higgs mechanism, check out the following insightful videos.
The first video titled "The Higgs Mechanism Explained | Space Time | PBS Digital Studios" provides a detailed overview of the subject, making complex topics accessible.
The second video, "The Crazy Mass-Giving Mechanism of the Higgs Field Simplified," offers a simplified explanation, ensuring that viewers can grasp this crucial concept in particle physics.