# Exploring the Concept of BC in Geometry: A Fun Challenge
Written on
Chapter 1: The Geometry Challenge
We’re on the verge of reaching 40k followers, and I can’t wait for us to hit 100k soon! If you enjoy my work, consider buying me a coffee—your support means the world!
Now, let’s tackle a fun geometry problem together!
I encourage you to pause here, grab some paper and a pen, and give it a shot. When you’re ready, continue for the solution!
Section 1.1: Understanding the Problem
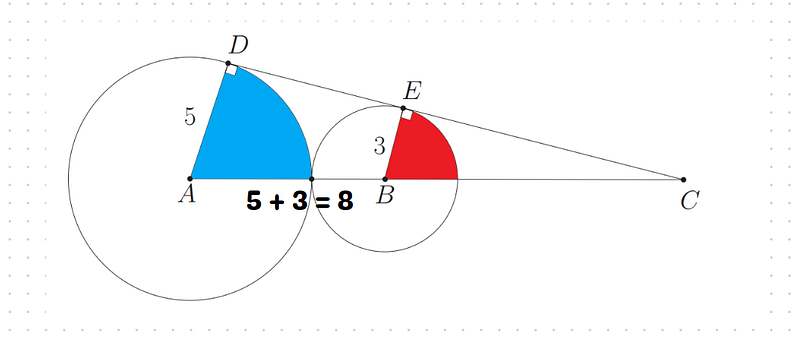
D and E are points where two circles, A and B, touch. Circle A has a radius of 5, while Circle B has a radius of 3. The distance AB is the sum of the two radii, giving us a length of 8.
The crux of this puzzle lies in recognizing the similarity of triangles. Specifically, the right triangles ADC and BEC share the same shape but differ in size.
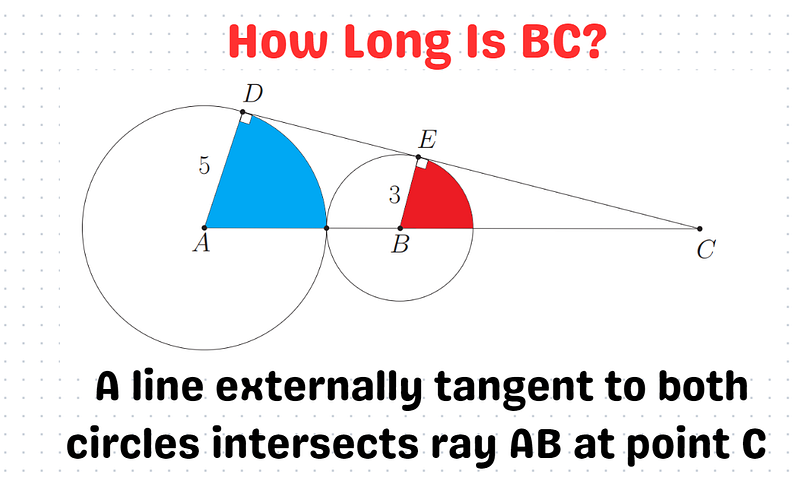
Thanks to their similarity, the ratios of corresponding sides will be equal.
Section 1.2: Solving the Challenge
We know that AC can be expressed as the sum of AB and BC, leading us to the equation AC = 8 + BC. The ratio of BE to AD is simply 3 to 5.
Using this information, we can set up the proportion:
BC / (BC + 8) = 3 / 5
Solving this gives us BC = 12. And that’s the solution!
How fascinating is that? I’d love to hear your thoughts on this problem—leave a comment below!
Chapter 2: Further Exploration
The first video delves into the concept of chronological time, explaining the differences between BC, AD, BCE, and CE.
The second video provides a clear explanation of AD and BC, along with insights into CE and BCE.
Thank you for engaging with this geometry challenge! Remember, if you found this article helpful, please give it a clap.

If you appreciate my work and want to support my writing journey, consider buying me a coffee! Your generosity is greatly appreciated. Happy solving, and I look forward to our next challenge!