Defining Entropy

The classical definition of entropy in physics, denoted as S, is formulated as:

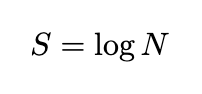
Here, N represents the number of states available to a specific system. While this definition may appear straightforward, the complexities arise in understanding what we mean by “the number of states” and how we quantify this. Intuitively, one might assume a system has only one state, leading to the conclusion that entropy is always 0.

To effectively define entropy, we must expand our view beyond the system in question. Instead of consistently counting one state, we must account for the number of states that share common features with our system.

In essence, entropy counts the number of states that possess relevant characteristics while disregarding those that are irrelevant. Consequently, computing entropy necessitates categorizing the details of a system into relevant and irrelevant aspects. This categorization allows entropy to quantify our lack of knowledge.

Consider an example: suppose our physical system is represented by the following 100 digits:

7607112435 2843082689 9802682604 6187032954 4947902850

1573993961 7914882059 7238334626 4832397985 3562951413

These numbers appear random. If we consider only the fact that there are 100 digits and disregard the specific numbers, the entropy would simply be:

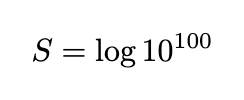
However, these digits actually represent the first 100 digits of π in reverse. If we define our system as precisely those digits, only one state can describe it, leading to an entropy value of 0.

While this example illustrates the challenge of defining entropy in isolation, it emphasizes the importance of identifying relevant and irrelevant quantities.

Relevant and Irrelevant Quantities

The distinction between relevant and irrelevant variables is crucial in physics:

• Relevant quantities: Macroscopic properties that remain relatively constant over time, usually measurable and controllable in experiments (e.g., total energy, volume, particle count).
• Irrelevant quantities: Microscopic aspects that fluctuate rapidly and are often not easily measurable (e.g., specific locations and velocities of particles).

Most systems can be categorized into these two groups. However, the definition of what constitutes rapid change is somewhat subjective; for instance, intermolecular forces operate faster than the blink of an eye, while intergalactic movements unfold over eons. If we can't clearly differentiate between these physical quantities, we conclude that the system is not in thermal equilibrium, rendering entropy ill-defined.

In summary, a more comprehensive definition of entropy is:

For a given system, entropy quantifies our ignorance regarding irrelevant quantities compared to relevant ones.

Addressing Common Misconceptions About Entropy

With this deeper understanding of entropy, we can tackle some prevalent misconceptions. For example, consider a messy floor. Does this indicate high or low entropy?

This question is, in fact, misleading. Similar to the digits of π, the question lacks clarity. We cannot meaningfully compute entropy without identifying the relevant and irrelevant variables. A chaotic space could represent a carefully designed artwork, making it difficult to categorize its entropy.

Another frequent scenario involves broken ceramics. Does the act of them falling increase entropy?

The answer is likely yes, but not due to their apparent chaos. Entropy tends to rise in everyday physical processes. The separation of ceramic pieces does not significantly contribute to our understanding of entropy.

Reflecting on our previous discussion about relevant versus irrelevant quantities, the broken pieces do not change or rearrange rapidly enough to thermalize. Thus, associating entropy with the patterns of broken ceramics is not very meaningful.

If we were to imagine a bizarre simulation where the same piece of ceramics breaks repeatedly, we could attempt to create a notion of entropy, but it would be an arbitrary concept.

Ultimately, we see that entropy does not encapsulate an objective, fundamental concept of disorder. So why do we often link entropy with chaos?

Entropy’s Link to Statistics and Information

To clarify this connection, we turn to statistics. Given a probability distribution p, we can calculate a value known as information entropy H. This quantity measures the randomness of the distribution and is expressed as:

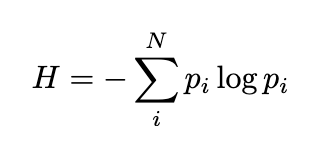
The sum is taken over all potential outcomes described by the distribution. How does this information entropy relate to the physicist’s interpretation of entropy? Notably, information entropy reaches its maximum when the distribution is uniform, with each probability equal to 1/N. The maximum value of information entropy is given by:

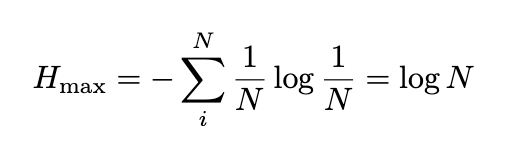
This relationship reveals that:

Entropy captures the randomness of irrelevant aspects of a system when we assume these aspects follow a uniform distribution.

With this understanding, we can summarize what entropy truly represents:

1. Analyze a system and categorize all physical variables as relevant or irrelevant.
2. Assume that the irrelevant quantities behave like random variables drawn from a uniform distribution.
3. Entropy measures our ignorance regarding these irrelevant variables.

In conclusion, entropy can only be assessed when we impose a statistical perspective on a system. However, no physical system strictly adheres to these statistical principles—quantum mechanics included. Thus, entropy serves as a gauge of the apparent “disorder” resulting from our incomplete understanding of the universe.