Captivating Visual Proofs in Mathematics: The Art of Understanding
Written on
Chapter 1: The Beauty of Mathematical Visualization
Mathematics is an extensive and continually evolving discipline. It encompasses an array of elements such as numbers, symbols, formulas, proofs, and diagrams. As one delves deeper into advanced mathematics, they encounter the rigorous foundations that support contemporary mathematical principles.
Despite the extensive effort mathematicians invest in crafting proofs from basic premises, there is a distinctive and fascinating method of demonstration known as "proof without words," or visual proof. This approach serves as an artistic representation, encapsulating a mathematical identity or statement in such a manner that its veracity becomes apparent without the need for verbal explanation.
Here are seven exquisite visual proofs that showcase this concept.
Section 1.1: Area of a Circle
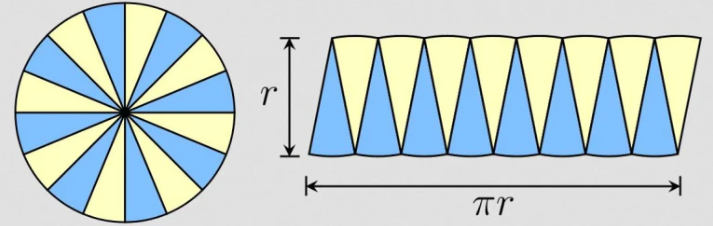
The area of a circle can be approximated by dividing it into a series of thin segments, which are then rearranged to form a shape resembling a rectangle. Each semicircle contributes to the width of the rectangle while the height corresponds to the radius of the circle. As the number of segments approaches infinity, the area of the circle approaches 2πr².
Section 1.2: Proving 2π > 6
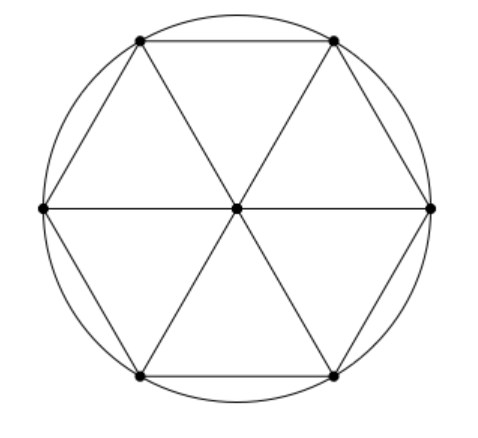
Consider the perimeter of both a circle and a hexagon. With a radius of 1, the circumference of the circle is 2π, while the hexagon consists of 6 equilateral triangles, each with a side length of 1, leading to a total perimeter of 6. According to Euclidean geometry, the shortest distance between two points is a straight line, which implies that the circumference exceeds the perimeter of the hexagon. Thus, 2π > 6.
Section 1.3: The Pythagorean Theorem
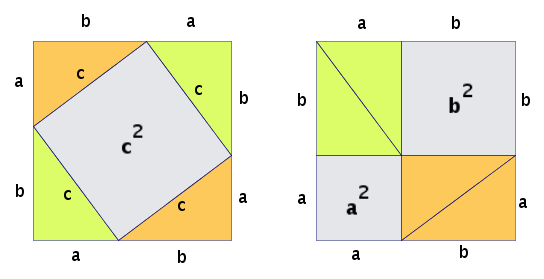
The Pythagorean theorem, expressed as a² + b² = c², is one of the most celebrated theorems in mathematics. It asserts that the sum of the squares of the two legs of a right triangle equals the square of the hypotenuse. The accompanying diagram illustrates a square with area c² at the center, surrounded by four triangles with sides a, b, and c. By rearranging these shapes, we can confirm that c² equals the combined areas of a² and b².
For further exploration, check out "Five Classic Proofs without Words" on YouTube, which beautifully elaborates on these elegant proofs.
Chapter 2: The Infinite and Beyond
Section 2.1: Summing Infinite Series
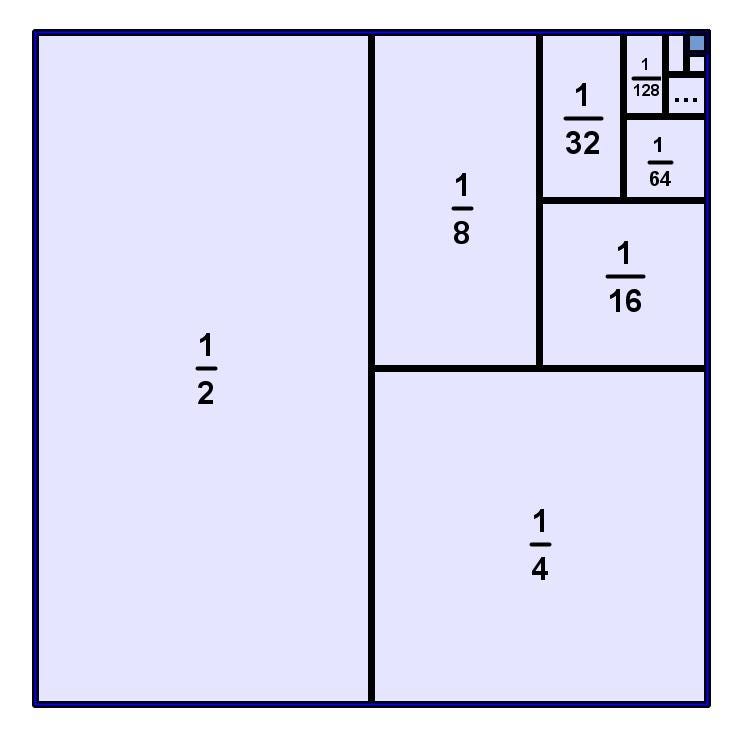
Starting from a square with a side length of 1, we can halve the area repeatedly, illustrating that the sum 1/2 + 1/4 + 1/8 + … converges to 1. This infinite series exemplifies how an infinite process can yield a finite result.
Section 2.2: More Complex Infinite Sums
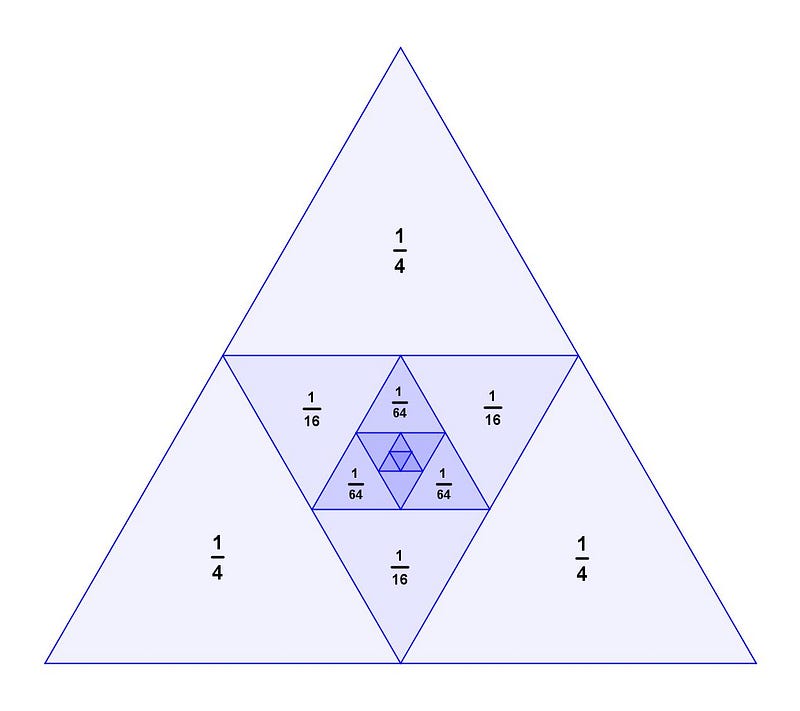
This proof requires a bit more complexity. We begin with an equilateral triangle of area 1, dividing it into four equal parts, and subsequently repeating this process indefinitely. The resulting series converges to a total of 1.
Section 2.3: The Sum of Odd Numbers
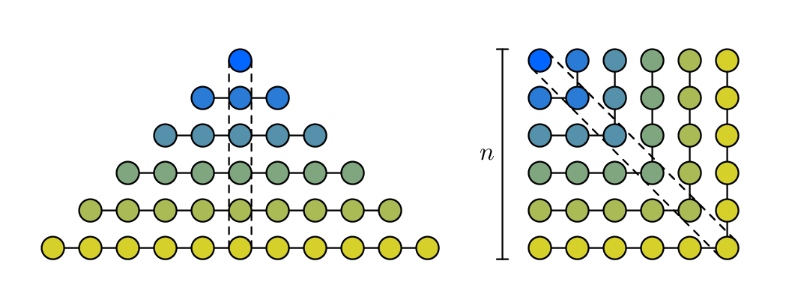
The diagram illustrates that the sum of the first n odd natural numbers results in n². This relationship can be visualized by arranging dots into a square formation.
For a deeper understanding, view "Beautiful Geometry behind Geometric Series" on YouTube. This video presents eight visual proofs that enhance comprehension of geometric series.
Section 2.4: Infinite Geometric Series Formula
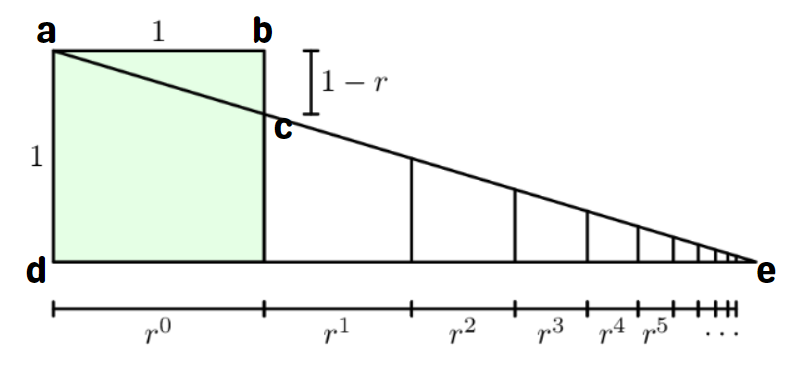
Finally, we conclude with a compelling proof of the formula for the infinite geometric series. Given that triangle ABC is similar to triangle EDA, the ratio of their sides is equal, leading to the formula: 1 + r + r² + r³ + … = 1/(1-r).

How remarkable is the realm of mathematics? What insights did you gain from this exploration? I invite you to share your thoughts below!
Thank you for engaging with this content. If you found it enlightening, consider sharing it with friends or supporting my work.

Your support means a lot! If you appreciate my writing, consider buying me a coffee to help sustain my efforts. Thank you!