Understanding the St. Petersburg Paradox: Pricing Uncertainty
Written on
Chapter 1: Introduction to the St. Petersburg Paradox
The St. Petersburg paradox marks a significant milestone in applied mathematics. Emerging in the early 18th century, it continues to engage some of the most brilliant minds in mathematics and philosophy. Why is it so noteworthy?
Humans frequently make decisions amid uncertainty, and one of the primary mathematical concepts developed to assist in these scenarios is expected value. To gain a deeper understanding of expected value, feel free to refer to my previous essay on the subject.
This paradox highlights the shortcomings of expected value theory, laying the groundwork for expected utility theory. Moreover, it has prompted philosophers and psychologists to reassess the nature of human decision-making. We still benefit from ongoing discussions surrounding this paradox.
In this essay, we will explore the origins of the St. Petersburg paradox, delve into its mathematical and philosophical foundations, and discuss potential solutions and their real-world applications. Let's begin our exploration.
Chapter 2: Origins of the St. Petersburg Paradox
The St. Petersburg paradox derives its name from one of the leading scientific journals of the 18th century: Commentarii Academiae Scientiarum Imperialis Petropolitanae.
In 1738, Daniel Bernoulli published a paper titled “Specimen Theoriae Novae de Mensura Sortis,” which presented a seemingly simple probability game that reveals counter-intuitive insights about pricing uncertainties through expected value theory.
However, Bernoulli did not originate this game; he learned about it from his cousin, Nicolaus Bernoulli, who first mentioned it in correspondence with Pierre Rémond de Montmort in 1713. Nicolaus's original game was quite complex, employing six dice. In this essay, we will focus on a simplified version instead.
Chapter 3: Analyzing the Game: How Much Should You Pay?
Imagine a scenario where a fair coin is flipped repeatedly until it shows heads. If heads appears on the first flip, you win $2; if it appears on the second flip, you win $4, and so forth.
In essence, the payout is $2^n, where n is the number of flips taken to get the first heads. The pressing question posed by Bernoulli is:
"How much would you be willing to pay to participate in this game?"
Of course, you wouldn’t expect to play for free—there’s always a cost. But how do we determine that cost?
Section 3.1: A Quick Overview of Expected Value
If you're not familiar with the concept of expected value, here's a brief overview: the expected value of a risky wager is calculated by multiplying each potential outcome's value by its probability and summing those products.
According to expected value theory, your decision-making regarding the wager should focus on maximizing the expected value. Thus, a higher expected value indicates a greater worth for the bet. Now, let's calculate the expected value for this intriguing game.
Chapter 4: Revealing the Paradox
A fair coin has a 50% chance of landing heads. Winning $2 on the first flip corresponds to this 50% probability. There’s a 25% chance of tails on the first flip followed by heads on the second, resulting in a $4 payout. Extending this logic, we arrive at a summation series:
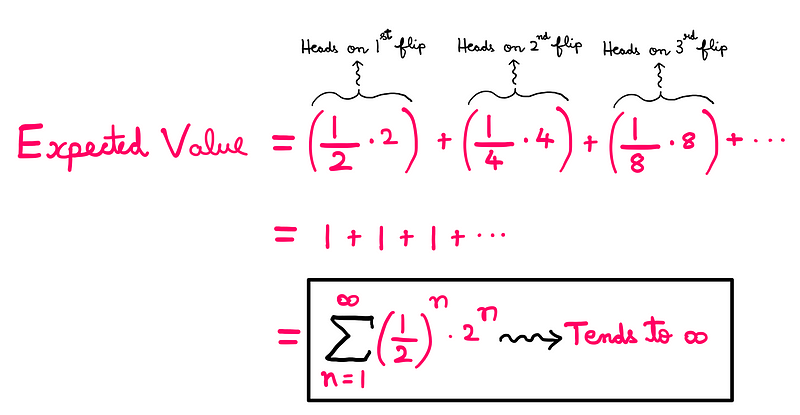
Thus, the expected value of our game approaches infinity. Should this mean you ought to risk everything for a chance to play? That seems unreasonable, doesn’t it?
My instinct suggests I wouldn’t pay more than $5 to play. This disparity is what we term the St. Petersburg paradox, illustrating the gap between intuitive judgments of value and the mathematical interpretation of expected value.
It's important to note that this paradox does not present a logical inconsistency; rather, it falls under the category of veridical paradoxes. So, how can we reconcile this disconnection? An associate of Nicolaus Bernoulli offered a solution.
Chapter 5: Solutions to the St. Petersburg Paradox
Before Daniel Bernoulli’s paper was published, a mathematician from Geneva named Gabriel Cramer had encountered the problem in a Montmort publication. He proposed a simplified version of the St. Petersburg game that we are examining.
Cramer’s solution ventured beyond traditional mathematics, influencing modern applied mathematics and decision theory. He posited that monetary value is subjective, suggesting that expected value should not dictate betting decisions.
Instead, he argued that the value of money diminishes beyond a certain threshold. For instance, $20 million does not provide ten million more value than $10 million, since the first ten million suffices to meet a rational player’s needs and desires.
Cramer proposed two methods for addressing the St. Petersburg paradox.
Section 5.1: The Upper Bound Solution
Despite the expected value trending toward infinity, we must acknowledge that real-world monetary resources are limited. Thus, Cramer suggested establishing an upper limit on the game's potential winnings.
By setting 2^m as the upper limit, the game concludes if heads appears on or after the m-th flip. This modification allows for an infinite number of possibilities while keeping the outcome and expected value finite.
However, this approach is not without its challenges. Cramer recognized that asserting an upper boundary is contentious. Many mathematicians argue that finite resources do not invalidate the concept of an infinite expected value.
Moreover, the issue resurfaces when considering infinite real-world resources.
Imagine substituting dollars with grains of sand as the prize. If you win 2 grains of sand for heads on the first flip, the notion of an upper limit becomes untenable, and the paradox re-emerges. This is where Cramer’s second solution proves useful.
Section 5.2: The Moral Value Solution
In this alternative approach, instead of imposing a limit, Cramer reduced the pace at which monetary value grows by defining the moral value of goods as the square root of their corresponding mathematical quantities.
If this seems abstract, here’s how the improvised summation series appears:
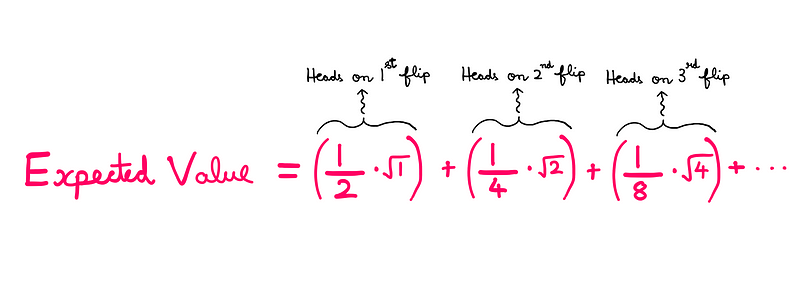
Using this framework, Cramer estimated the value of the bet at approximately $2.9—revealing that my initial intuition was off by $2.1.
This definition of moral value implies that additional wealth never equates to zero value; instead, the benefits diminish as wealth increases. Cramer inadvertently introduced what contemporary economists term decreasing marginal utility.
In essence, this laid the groundwork for expected utility theory.
Chapter 6: Conclusion
In his 1738 paper, Daniel Bernoulli proposed a similar solution, defining the utility of wealth as the logarithm of the monetary amount. As wealth accumulates, the value of money saturates along a logarithmic curve. Bernoulli acknowledged Cramer’s concept as closely aligned with his own, giving him credit in his work.
Even after all these years, the St. Petersburg paradox remains a rich source of insight and exploration. While it may seem abstract with limited practical application, I can assure you that valuable lessons lie beneath the surface.
A significant portion of my income can be traced back to the insights gained from studying this paradox. The latest advancements in addressing the St. Petersburg paradox are rooted in Ergodicity theory.
Since Ergodicity is a complex concept that warrants its own discussion, I intend to elaborate on it in a subsequent essay.
If you appreciate my work, please consider supporting me through claps, follows, or subscriptions.
Further reading that may pique your interest:
- Understanding the Raven Paradox
- Grasping Statistical Significance
- Solving the Staircase Paradox
To support future endeavors, consider contributing on Patreon.
The first video titled "The St. Petersburg Paradox and Expected Utility" delves into the complexities of the paradox and its implications on decision-making.
The second video, "The St. Petersburg Paradox," offers an engaging overview of the paradox and its historical context.