Understanding the Mathematics of Language: Entropy, Redundancy, and Resilience
Written on
Chapter 1: Introduction to Language and Mathematics
What does the term "Mathematics of Language" signify? Before delving into that, it's essential to identify the connections between language and mathematics. To illustrate this, let’s conduct a simple experiment: read the following encoded sentence:
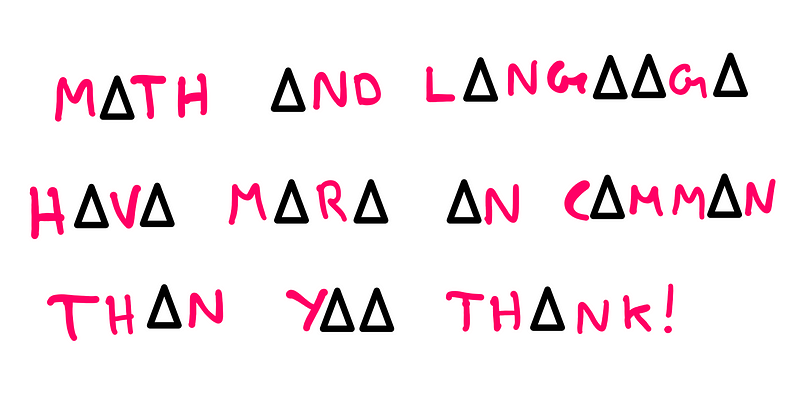
If you're a native English speaker, you likely deciphered the sentence above despite its encoding. This article explores how such language phenomena relate to mathematical concepts and how they can enhance our understanding.
Section 1.1: Analyzing Encoded Language
In the previous example, I substituted all vowels in the sentence with a triangle symbol. Thus, to comprehend it, one simply needed to infer the missing vowels correctly. This demonstrates that we can still understand sentences even when certain letters (in this case, vowels) are omitted. If you’re doubtful about this assertion, let's validate it again using text shorthand:
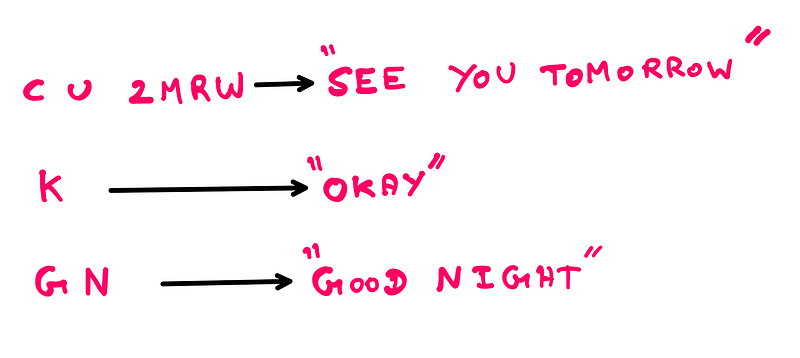
If we can convey messages more effectively with fewer letters, why do we continue to use elaborate sentences filled with complex grammatical structures? To answer this, we must first grasp the concept of Shannon entropy.
Section 1.2: Claude Shannon and His Contributions
Claude Elwood Shannon is arguably one of the most underappreciated figures in science.

At the age of 21, as a master's student, he fundamentally shaped an entire field known as information theory through his thesis. Shannon not only posed groundbreaking questions but also provided significant answers, leading to advancements that catalyzed the digital computing revolution.
Shannon’s work remains integral to our modern technological devices, influencing innovations even today. Among his numerous contributions, two are particularly relevant here:
- Development of Shannon entropy as a measure of information content within a message.
- Analysis of the entropy associated with printed English.
Chapter 2: Understanding Shannon Entropy
Shannon defined information entropy, now known as Shannon entropy, as a metric for the amount of information that can be conveyed by a message. To grasp this concept intuitively, consider a coin that has "heads" on both sides. In this instance, we are interested in how many questions we need to ask to determine the outcome of a toss.
When tossing such a biased coin, no questions are necessary, as the outcome will always be "heads." Thus, according to Shannon’s framework, this message system has zero entropy.
Conversely, with a fair coin that has "heads" on one side and "tails" on the other, tossing it twice requires two questions to ascertain the results of each toss, giving this information system two bits of entropy. It's important to note that the term "bit" was first introduced in Shannon's thesis, attributed to fellow mathematician John Tukey.
Now, consider a two-letter English word with unknown letters. How many questions do we need to ask to identify it? For instance, we could start by determining if the first letter falls within the first or second half of the alphabet.
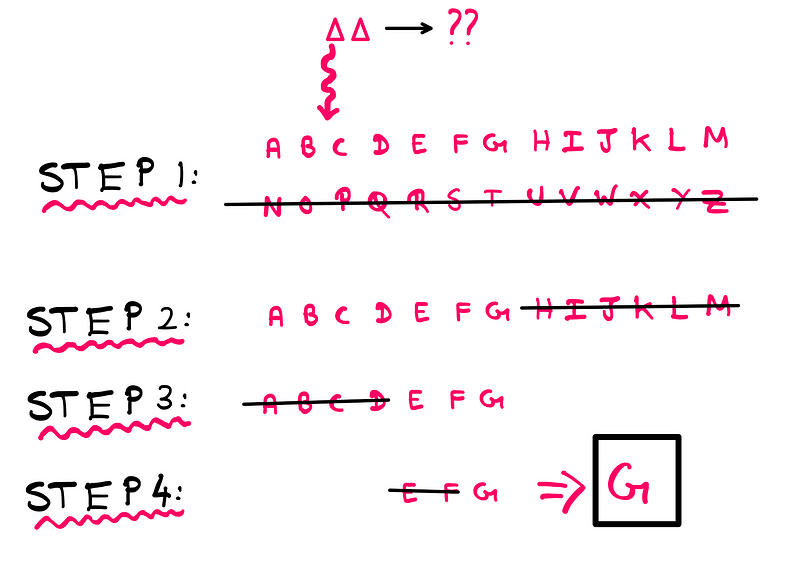
In this scenario, we can identify the word in four steps, indicating that it possesses four bits of entropy. If it takes five additional steps to discover the second letter as "O," then the word "GO" carries a total of nine bits of entropy.
Section 2.1: The Role of Order and Randomness
The word "GO" containing nine bits of entropy assumes the occurrence of English letters is random. However, the English language provides structure through grammar and conventions. For instance:
- The letter "E" appears significantly more frequently than "Z."
- The letter "Q" is typically followed by "U."
Shannon was intrigued by these patterns and, through statistical analysis and experimentation, calculated that the average entropy of the English language is 2.62 bits per letter.
Chapter 3: The Implications of Redundancy in Language
Shannon sought to utilize these findings to create models for predicting and compressing information in the English language, thereby maximizing the entropy that could be accommodated within a particular bandwidth. Generally, natural phenomena tend to show an increase in entropy over time, but the evolution of the English spelling system suggests a move from higher to lower entropy.
This paradox arises because humans (and nature) have distinct intentions. When the significance of a message rises, we often resort to longer formulations filled with redundancies to ensure that the core message remains intact, even if parts of it are omitted.
For example, when texting a friend about a party, you might use concise messages. However, when applying for a job, you would likely prioritize detail and clarity, resulting in more redundancy.
Section 3.1: The Resilience of Language
The inherent redundancy of the English language, combined with our cognitive inclination to seek patterns, allows us to understand sentences even when they are missing letters or vowels. As individuals who optimize efficiency, we might believe there's room for improvement in our language use. However, historically, the trend has been the opposite.
The gradual increase in structural redundancy has made English easier to use over time, leading to enhanced resilience against communication errors. This adaptability explains why English has flourished as a global Lingua Franca.
Final Thoughts
Have you ever pondered why a scratched CD usually functions properly? The answer lies in the redundant bits and error correction protocols embedded within them, making them resilient to errors. This concept extends beyond just the English language.
The takeaway from this discussion is that not everything should be optimized for efficiency. Sometimes, prioritizing resilience and robustness is more crucial than mere efficiency!
Reference: Claude Shannon (research paper).
I hope you found this exploration engaging and informative. If you wish to support my work as an author, consider showing appreciation through likes, follows, and subscriptions. For further reading, you might enjoy "Why Does The Human Brain Miss The Second ‘The’?" and "Are We Living In A Simulation?"