Chapter 1: Introduction to Implicit Differentiation

Implicit differentiation is a crucial concept in calculus. In many scenarios, we encounter functions expressed as y = f(x), where y is defined explicitly in terms of the independent variable x. In such cases, deriving the function is relatively straightforward, with the derivative noted as dy/dx or y’(x), achieved through standard differentiation techniques.

However, not every function can be neatly expressed in this explicit format. Often, we find ourselves dealing with functions that are more complex, such as g(x, y) = c. Here, g(x, y) incorporates both variables x and y, but y remains a function of x, making x the independent variable.

So, how do we approach these situations? Is it possible to find the derivative? The answer is affirmative; however, the method for calculating it differs slightly. Let’s explore this through an example:

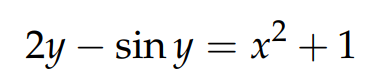
Equation 1

This equation represents an implicit function where y cannot be completely isolated. It takes the form g(y) = f(x), indicating that to find the derivative y’(x), we must apply some clever manipulations. A fundamental principle from differentiation states that if y = f(x) and there’s a function g(y), the derivative of g(y) with respect to x equals the derivative of y with respect to x multiplied by the derivative of g with respect to y. This is known as the chain rule, expressed as follows:

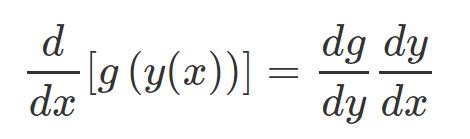
Since derivatives act as “linear operators,” meaning that the derivative of a sum of terms equals the sum of their derivatives, we can differentiate both sides of Equation 1:

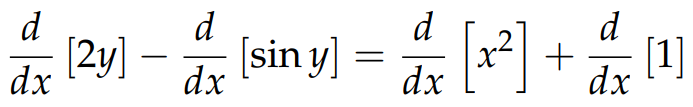
Next, we apply the chain rule to the functions of y on the left side, while utilizing standard differentiation techniques on the right side, leading us to:

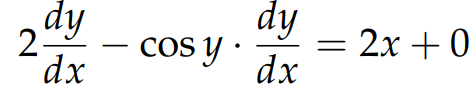
The final step is to observe that the term dy/dx is common on the left side. Rearranging the equation in terms of dy/dx results in:

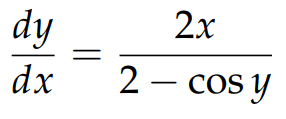
Upon close inspection, we see that this is precisely the derivative y’(x) we sought! Thus, we were able to differentiate Equation 1 and derive an expression involving both x and y. This implies that to find the derivative at a specific point (x0, y0), we need to input two values instead of the usual one, which is typical for explicit functions. Nevertheless, this process is indeed feasible.

Another Example

Consider the following:

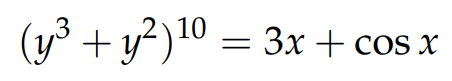
Equation 2

Similar to before, we apply the chain rule on the left side, resulting in:

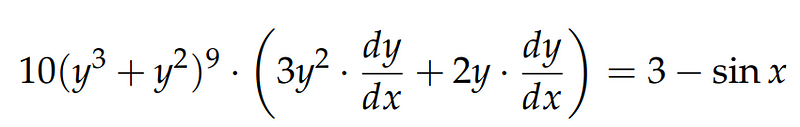
This can then be rearranged conveniently into:

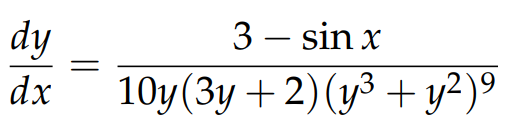
Lastly, let’s analyze a case where x and y are intertwined:

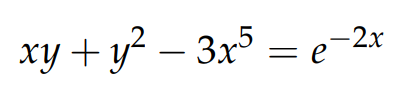
Equation 3

Here, the term xy requires us to employ both the chain and product rules during differentiation. This gives us:

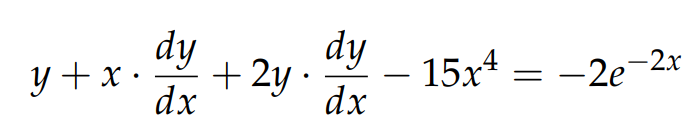
Rearranging this yields:

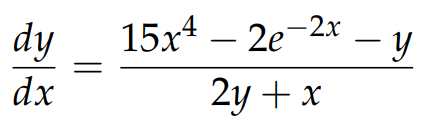
From these instances, we can conclude that the standard differentiation rules apply to implicit functions as well, including relations like x² + y² = 1, which are not technically functions. For example, using implicit differentiation on x² + y² = 1 yields:

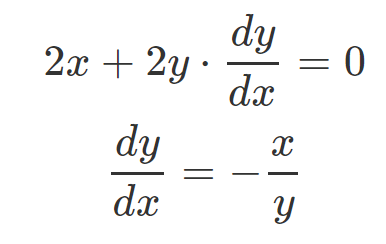
This may initially seem perplexing, but consider that x² + y² = 1 represents a circle with a radius of 1. By selecting a point (x0, y0) that satisfies this equation, we can compute the derivative at that location. For instance, at the point (0, 1), we find dy/dx = 0, indicating a horizontal tangent line (zero slope). Conversely, at the point (1, 0), we encounter dy/dx = -1/0, which is undefined because division by zero is not permissible. However, as we approach (1, 0), the slope tends to become infinite, resulting in a vertical tangent line.

Now, let's choose another point that satisfies the equation:

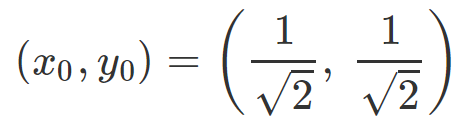
This point lies halfway along the first quadrant of the circle and forms a 45-degree angle with the horizontal and vertical axes if traced from the origin. Through geometric reasoning, we deduce that a tangent line at this point will have a negative slope, also forming a 45-degree angle with the horizontal. To confirm this, we can substitute these values into our dy/dx expression, yielding dy/dx = -1. This indicates a slope of -1, meaning that for every unit increase in x, y decreases by one unit, producing an angle of inclination of -45 degrees, as anticipated.

This straightforward example involving the circle highlights the efficacy of implicit differentiation.

Chapter 2: Visualizing Implicit Differentiation

This video provides a concise overview of implicit differentiation, emphasizing its application and importance in calculus.

In this video, you’ll find a thorough explanation of implicit differentiation, offering clear examples to enhance understanding.