Exploring the Sum of Infinitely Many Angles in Mathematics
Written on
Chapter 1: The Infinite Angle Conundrum
Have you ever wondered what the result would be if we continued to add angles indefinitely? As these angles become increasingly smaller, they approach zero over an infinite timeline. However, what does this imply for their summation? Join us on this mathematical journey for a fascinating exploration!
Before diving into the details, consider expressing the angle using trigonometric functions. By comparing each function to a simpler term and leveraging insights from real analysis, you might uncover something intriguing. It’s a good idea to pause here, grab some pen and paper, and attempt to solve this before proceeding!
Solution
Let’s start by examining the initial set of angles.

As we analyze these angles, we discover that the tangent of the nth angle corresponds to 1/n. This leads us to the problem of calculating the infinite sum of these angles!
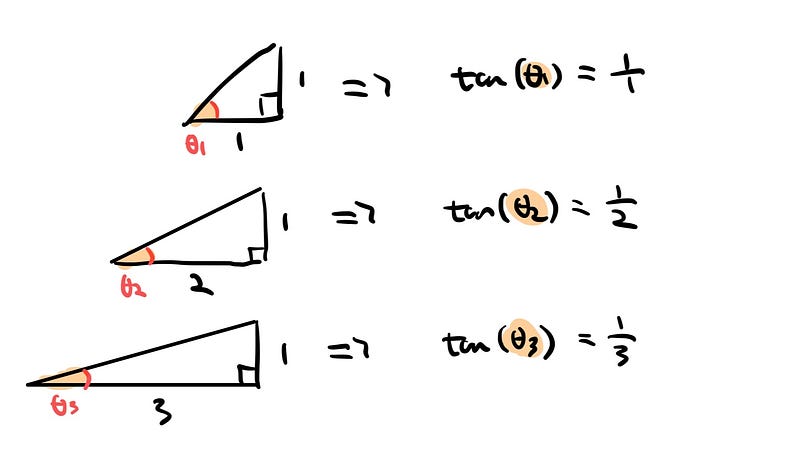
Take a moment to ponder this challenge if you wish!
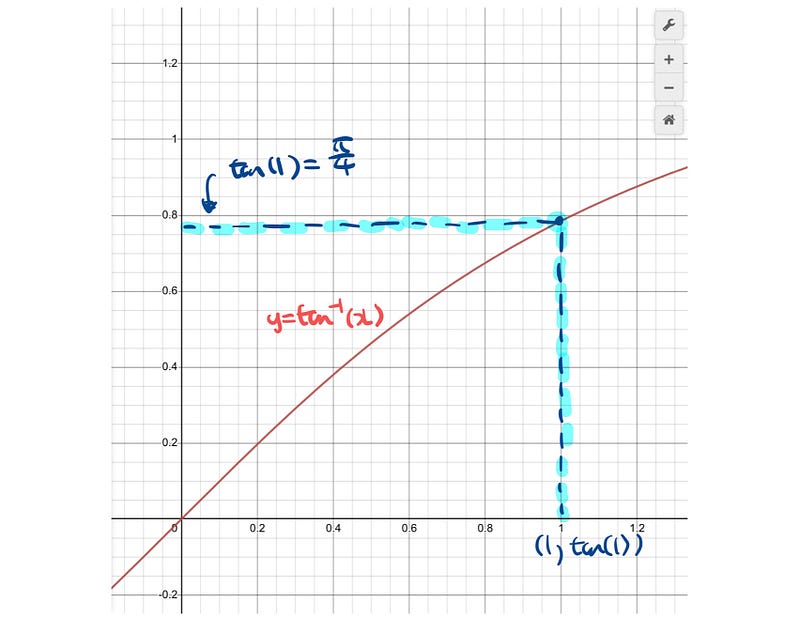
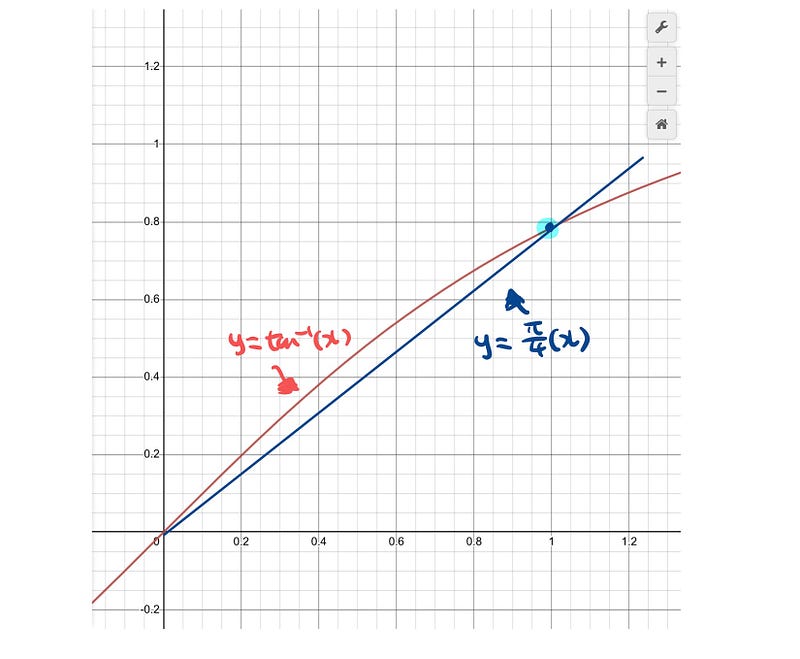
Let’s delve into the inverse tangent function for further clarity.
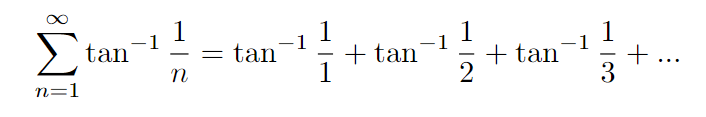
The red curve illustrates our function, starting with x = 1 as our point of interest.
The corresponding y-value at this point is π/4. If we draw a line from the origin to this point, we can derive the following equation.
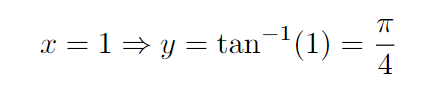
Notice how the graph of the inverse tangent is consistently greater than or equal to the linear function connecting the origin to the point (1, π/4)?

This relationship holds true for every point from 0 to 1, showcasing that the inverse tangent function remains above the linear equation.
We can further confirm this pattern through individual evaluations of initial points.
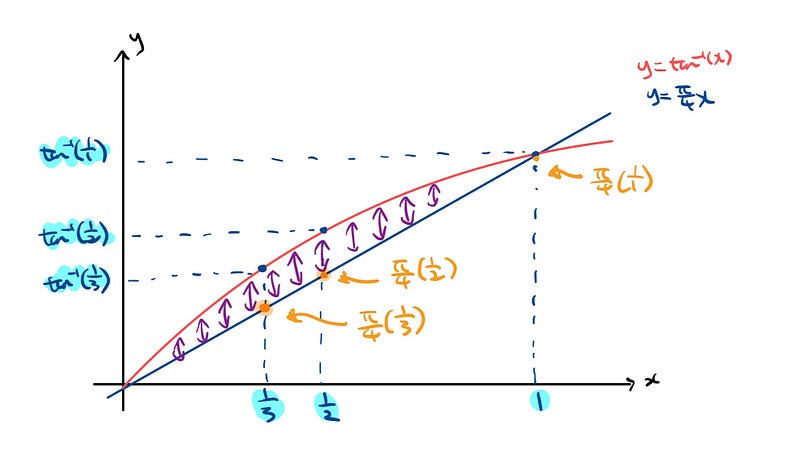
This trend continues indefinitely, applicable to any nth term and the summation of these terms.
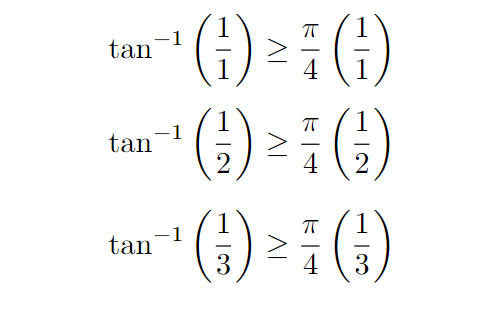
Does the expression on the right seem familiar? For those familiar with undergraduate real analysis, this is known as the harmonic series. According to the integral test, this sum diverges, indicating it grows infinitely large!
Consider this: multiplying an infinite value by a positive real number still results in an infinite value. Thus, since our sum exceeds an infinite sum, we can conclude that the final answer is infinity! To articulate this rigorously, we affirm that the sum diverges.
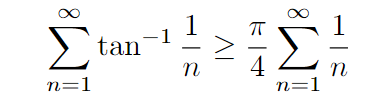
Isn’t that fascinating? Here’s a delightful image of some mice enjoying cheese!
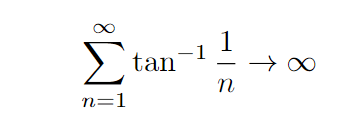
Math Puzzles
Delve into intriguing problems involving Algebra, Geometry, Calculus, Number Theory, and more!
Thank you for engaging with this exploration! If you found this discussion enlightening, please show your appreciation by giving it a clap. You can also support my work on Ko-fi!
Love, Bella 😊
Chapter 2: Understanding Infinite Series
In the video titled "What is the Sum of Infinitely Many Angles?" we further dissect the concept of summing infinite angles.
Additionally, the video "Sum of Infinite Geometric Series" elaborates on the principles behind infinite series and their implications.