Kepler’s Contributions to Orbital Mechanics

Johannes Kepler made groundbreaking contributions to orbital mechanics. Utilizing data from Tycho Brahe, who gathered information without a telescope, Kepler formulated three laws that have become the bedrock of this field. These laws elegantly explained planetary movements, fundamentally altering our understanding of the cosmos.

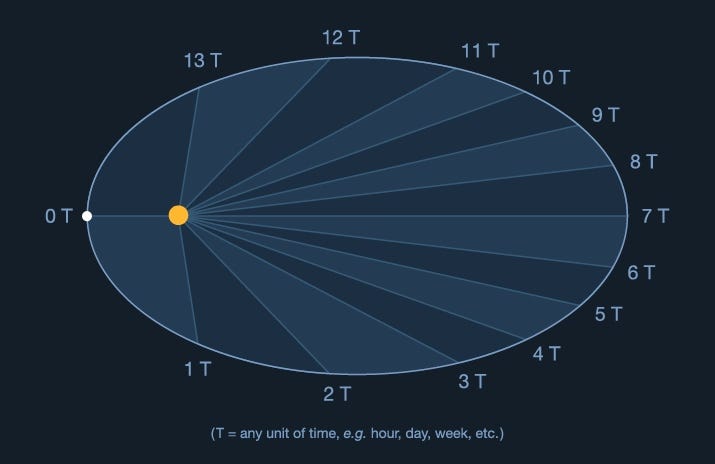
1. The Law of Orbits: All planets travel in elliptical paths, with the sun positioned at one focus.
2. The Law of Areas: A line connecting a planet and the sun sweeps out equal areas during equal time intervals.
3. The Law of Periods: The square of a planet’s orbital period is directly proportional to the cube of the semi-major axis of its orbit.

If Kepler’s laws emerged from observing planetary motions from Earth, how do they apply to satellites? The planets themselves can be viewed as satellites of the sun, and these laws similarly govern satellites orbiting other celestial bodies, such as the International Space Station in low Earth orbit or geostationary satellites.

Kepler’s laws hold true primarily due to gravity. One focus of an elliptical orbit is always a mass; in our solar system, that mass is the sun. For different orbital configurations, the focal point might be Earth, the Moon, etc.

Now that we’ve reviewed the basics, let’s return to our initial question: can a satellite orbit around an empty space? According to the principles of orbital mechanics, the answer is no.

The Loophole in Orbital Mechanics

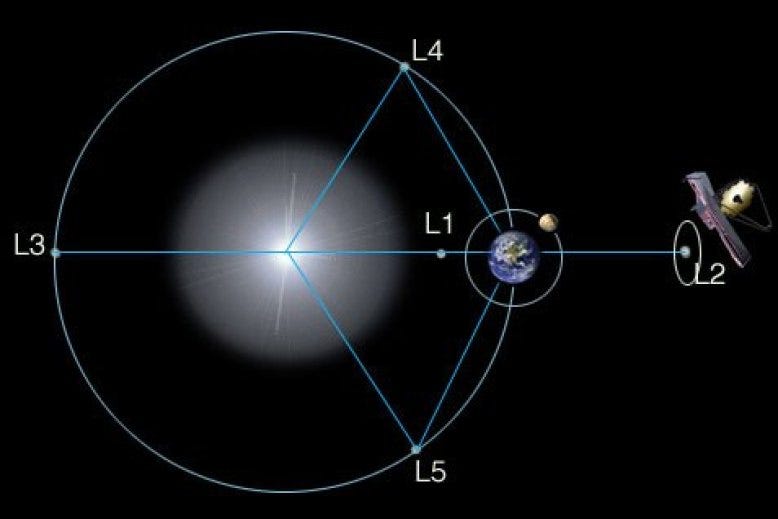
Every principle has its exceptions, and for orbital mechanics, that exception is the Lagrangian point.

Lagrange introduced these points in his work on the “General Three-Body Problem,” where he identified positions where the gravitational forces of two large masses balance with the centripetal force needed for a smaller object to maintain a stable position relative to them.

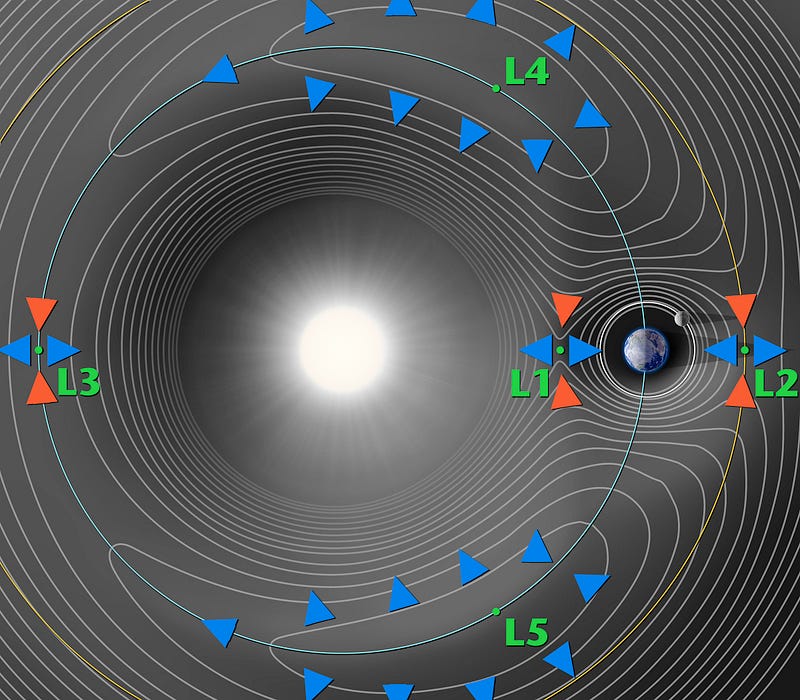
There are five Lagrangian points (L1-L5) in a specific orbital arrangement. A small satellite can effectively remain stationary relative to two larger bodies, such as the Sun and the Earth. While Lissajous orbits around these points can theoretically exhibit high stability, they are dynamically unstable in practice. Minor deviations from equilibrium can quickly escalate, necessitating propulsion systems for periodic adjustments.

NASA and ESA have utilized these unique orbits for various missions.

Navigating Lagrange Points

NASA has effectively explained Lagrangian points using relatable analogies. Imagine them as contours on a weather map—where the lines are closely spaced, the gravitational force is stronger; where they are farther apart, the force weakens.

Points L4 and L5 are akin to hilltops, while L1, L2, and L3 represent valleys. Satellites positioned at these Lagrangian points may gradually drift over time. A satellite at L4 or L5 tends to move toward the next contour line, leading to the influence of the Coriolis force—a phenomenon also responsible for the rotation of hurricanes on Earth—helping to stabilize its orbit around the Lagrange point.

In the video titled "How James Webb Orbits 'Nothing'," explore the unique orbits of satellites and how they can maintain stability in seemingly empty space.

The second video, "Why Spacecraft Are Using These Crazy Routes To The Moon," delves into the unconventional paths spacecraft take and the science behind these orbital maneuvers.