# Numerical Integration Techniques for ODEs in Python
Written on
Introduction to the Lorenz System
This article is designed to illustrate how to numerically solve and visualize the Lorenz system of ordinary differential equations (ODEs) using Python. The Lorenz equations represent a set of first-order, three-dimensional, coupled, nonlinear, and chaotic differential equations.

Photo by Andra C Taylor Jr on Unsplash
Results Overview
The numerical evaluation of the Lorenz ODEs employs the Runge-Kutta fourth-order (RK4) method. If you’re interested in a foundational overview of differential equations, as well as the Python implementation of the RK4 solver utilized for this simulation, please refer to related articles.
Discover how to numerically solve differential equations using Python and visualize chaotic systems.
Theory Behind the Lorenz Equations
Equations 1–3 present the set of differential equations formulated by Edward Lorenz, which serve as a simplified model for convective motion in a fluid layer created by temperature differences between its upper and lower surfaces.
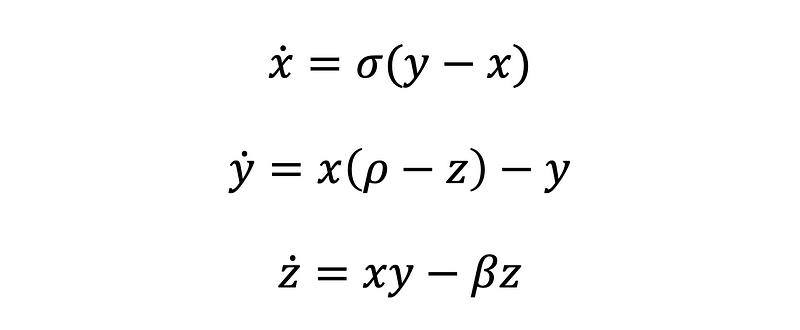
The state variables defined in these equations include:
- x: intensity of fluid convection
- y: temperature differential between rising and falling fluid
- z: nonlinearity of the temperature profile
The constant coefficients in the equations are:
- σ: related to the Prandtl number, a fluid property
- β: related to the Rayleigh number, which correlates with the temperature difference
- ρ: a geometric parameter pertinent to the fluid
Although Equations 1–3 do not explicitly depend on the nondimensional time parameter, they change over time, t. To analyze the system as time progresses, we evaluate the rates of change at specific time steps, leading to updates in the state variables x, y, and z based on the derived equations.
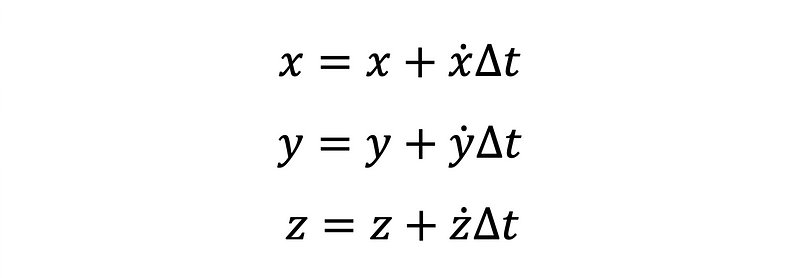
Python Implementation of the Lorenz System
Gist 1 illustrates how the Lorenz system can be represented in Python using a Numpy array. Ensure that the output from the lorenz function corresponds to Equations 1–3.
Solving this system with parameters σ = 10, β = 8/3, and ρ = 28 results in a fascinating phase trajectory. Below, you’ll find the Python code necessary to execute the simulation, including the RK4 function definition.
Learn how to solve ordinary differential equations using the Forward Euler method in Python.
Simulation Results
The state_history variable captures the evolution of the variables x, y, and z. By setting the initial conditions to [-8, 8, 27] and using Matplotlib to visualize the state variables in three dimensions, we can observe the Lorenz attractor, a trajectory that resembles a butterfly.
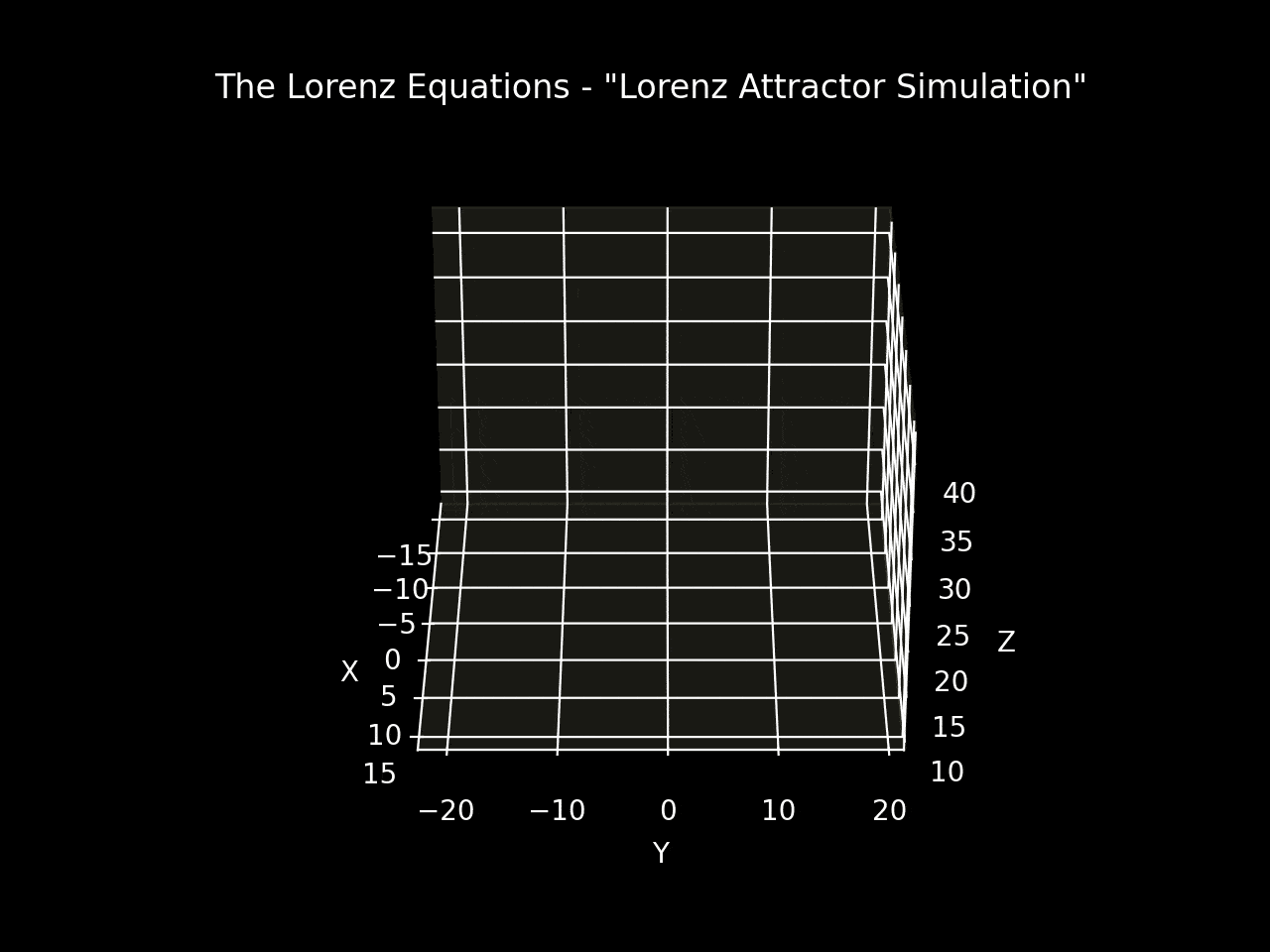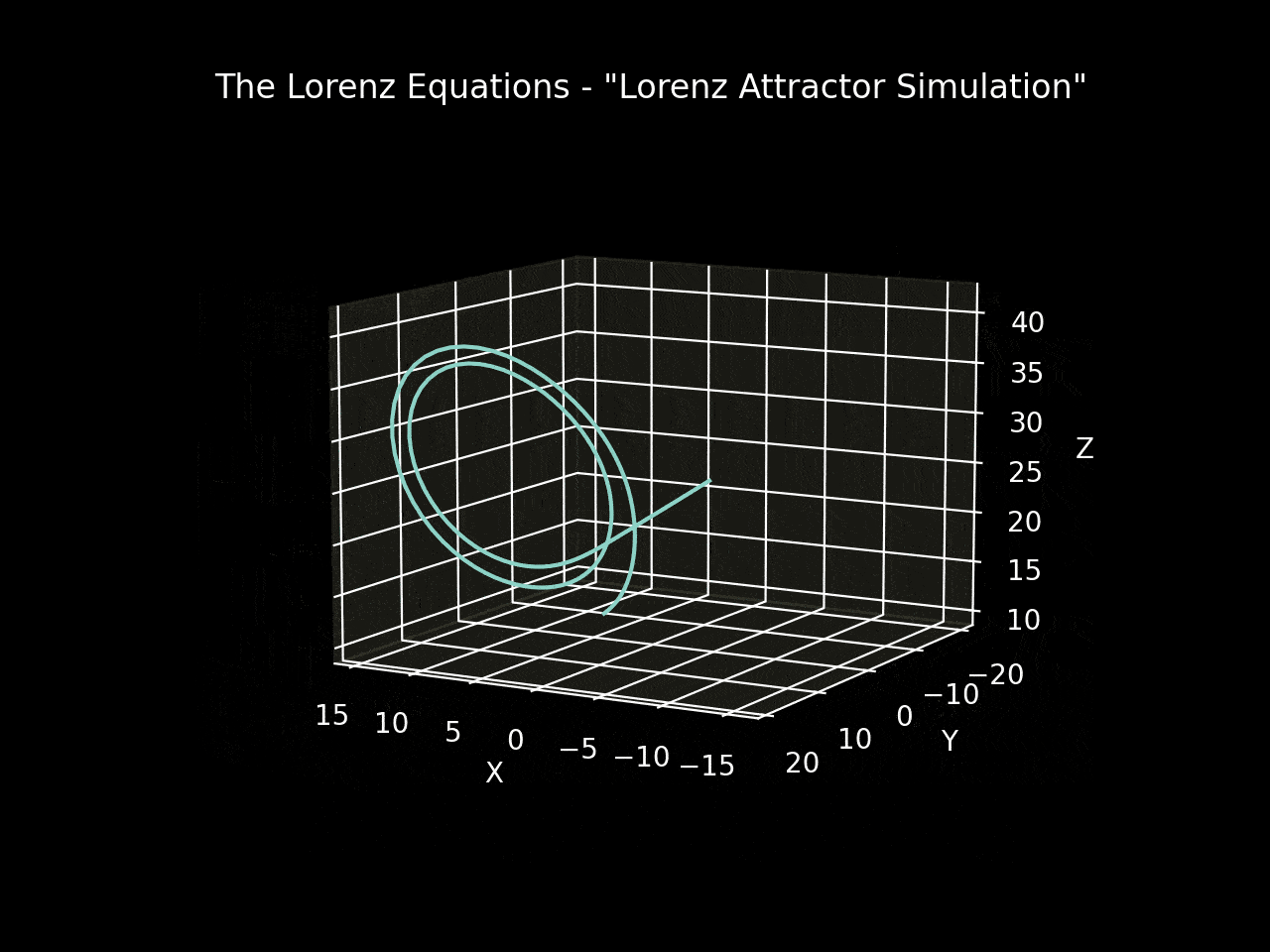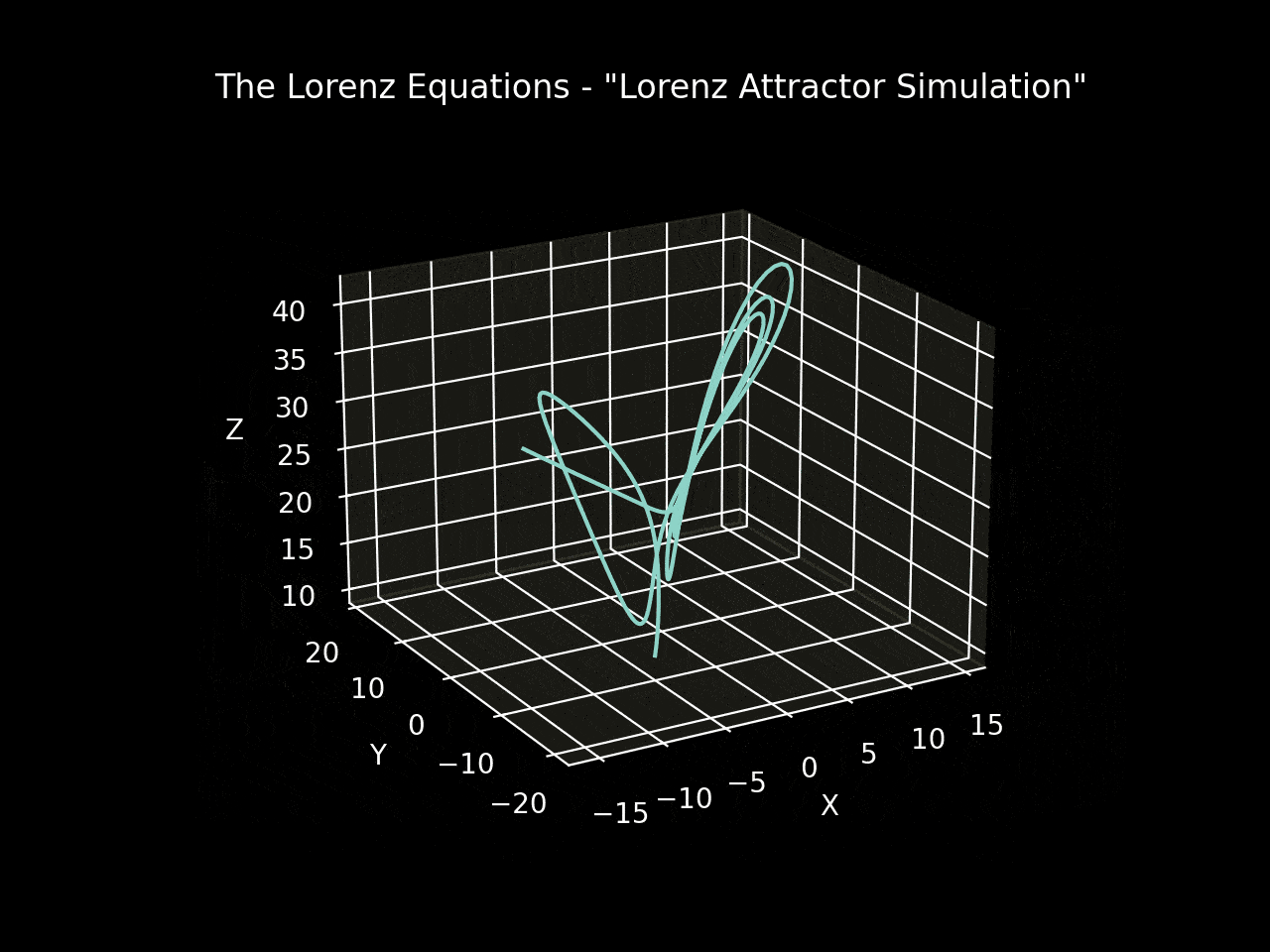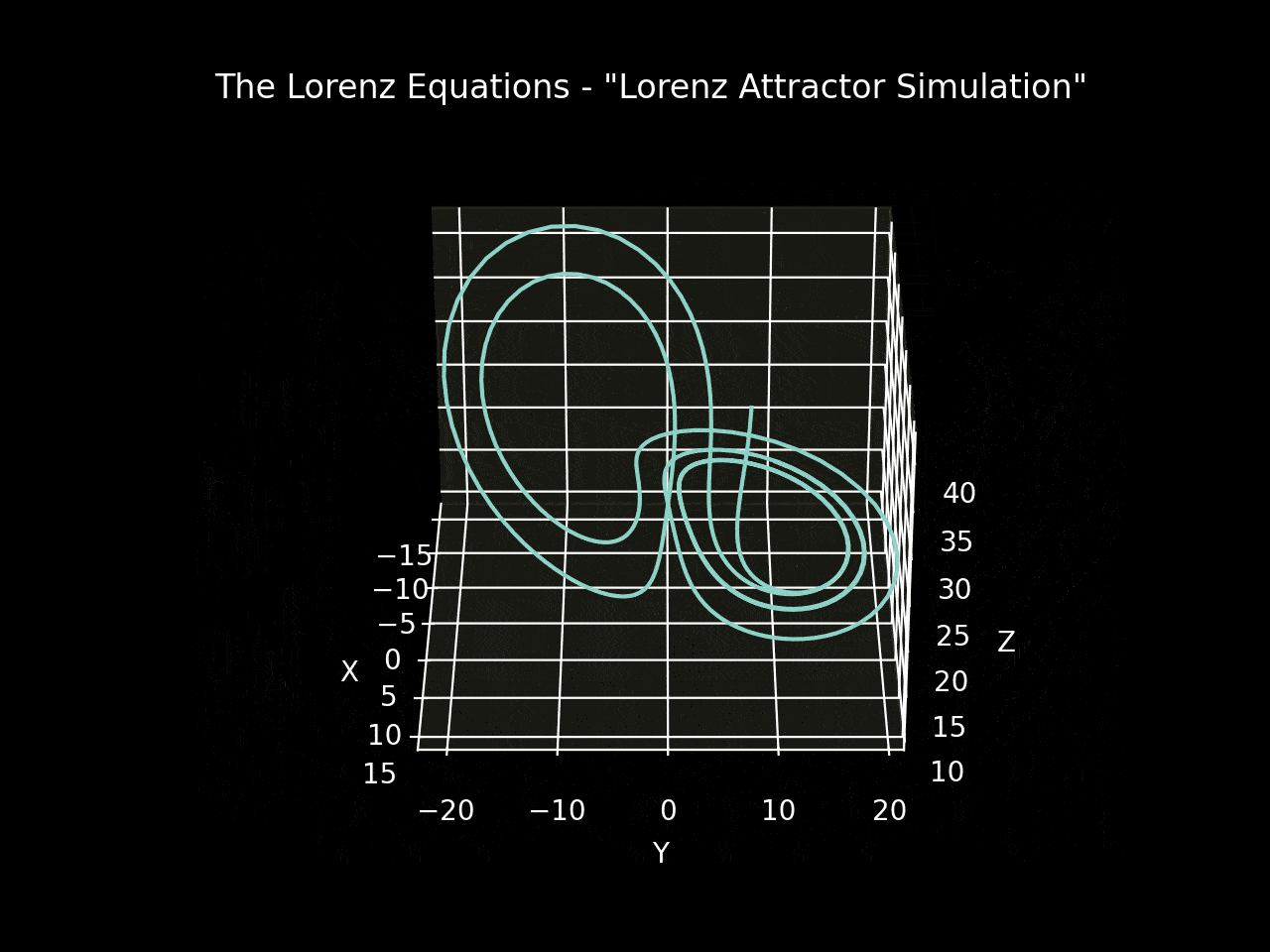
Figures 1 and 2 depict simulations with initial conditions of [-8, 8, 27] and parameters σ=10, β=(8/3), ρ=28 over a time range of [0, 4] seconds. Figure 3 illustrates a simulation of three systems initiated with identical conditions but slightly adjusted coefficients. Even though the overall shape may appear similar, the state variable values at any given time differ significantly, highlighting the sensitivity of deterministic systems and their potential unpredictability.
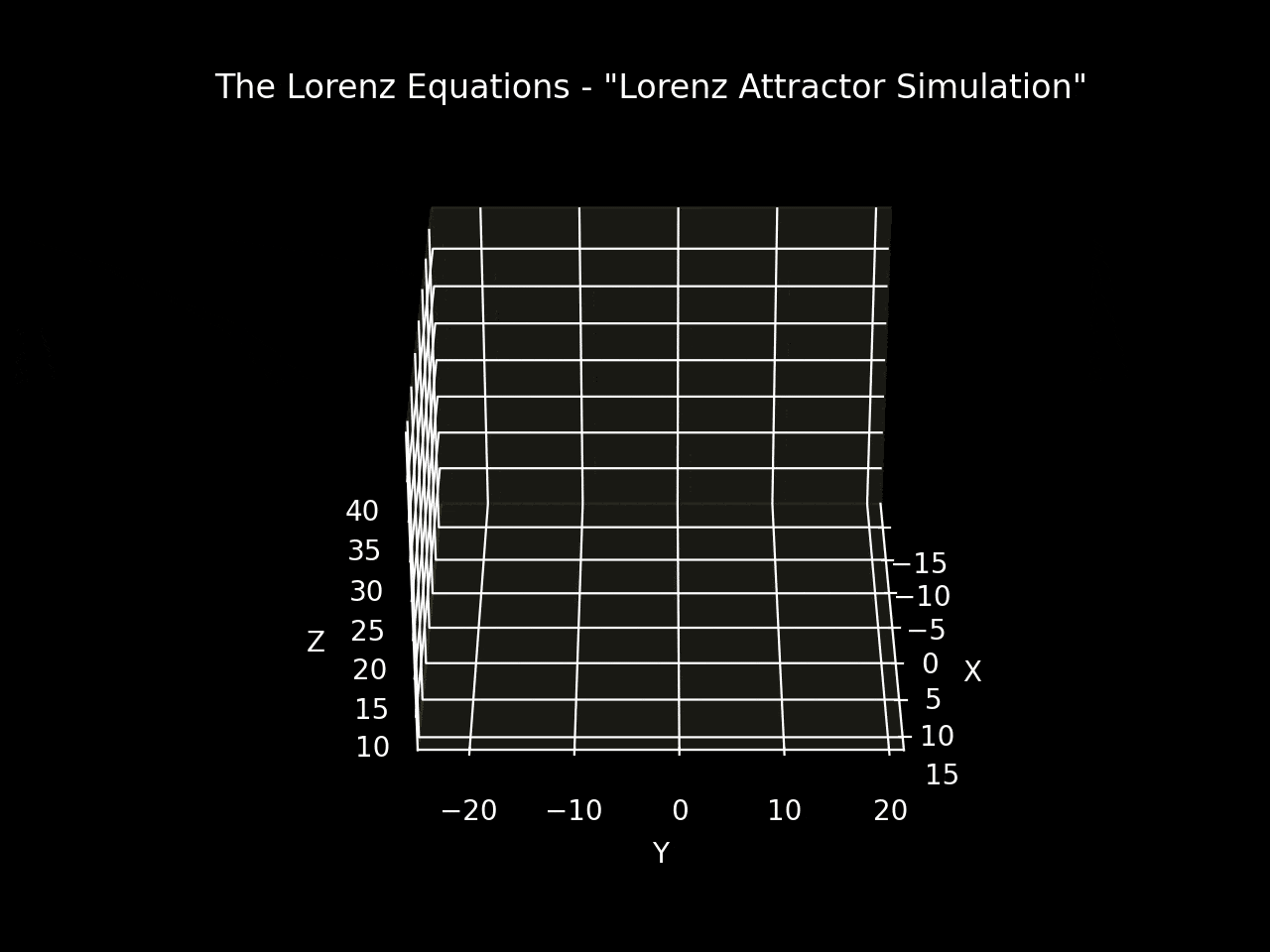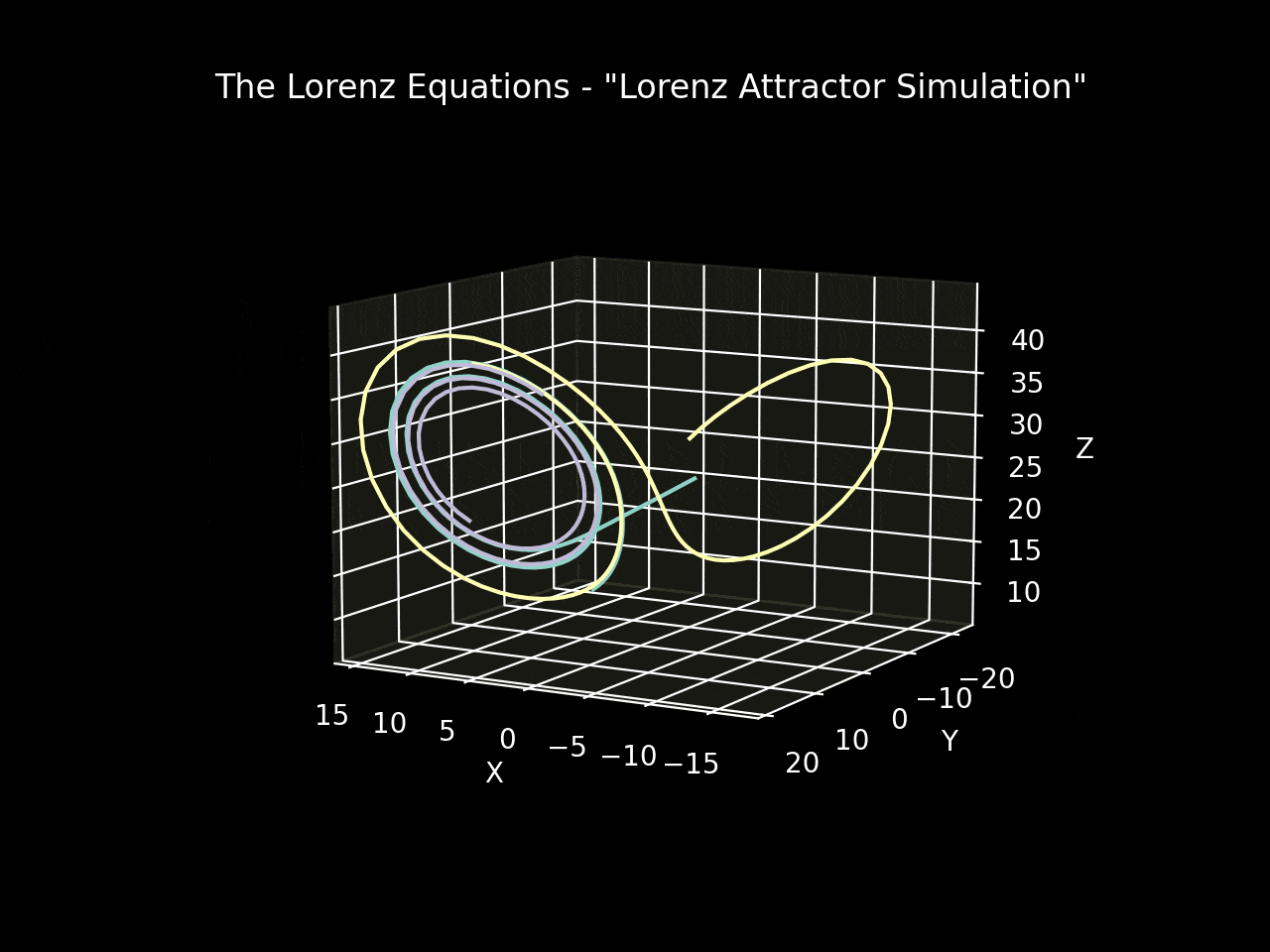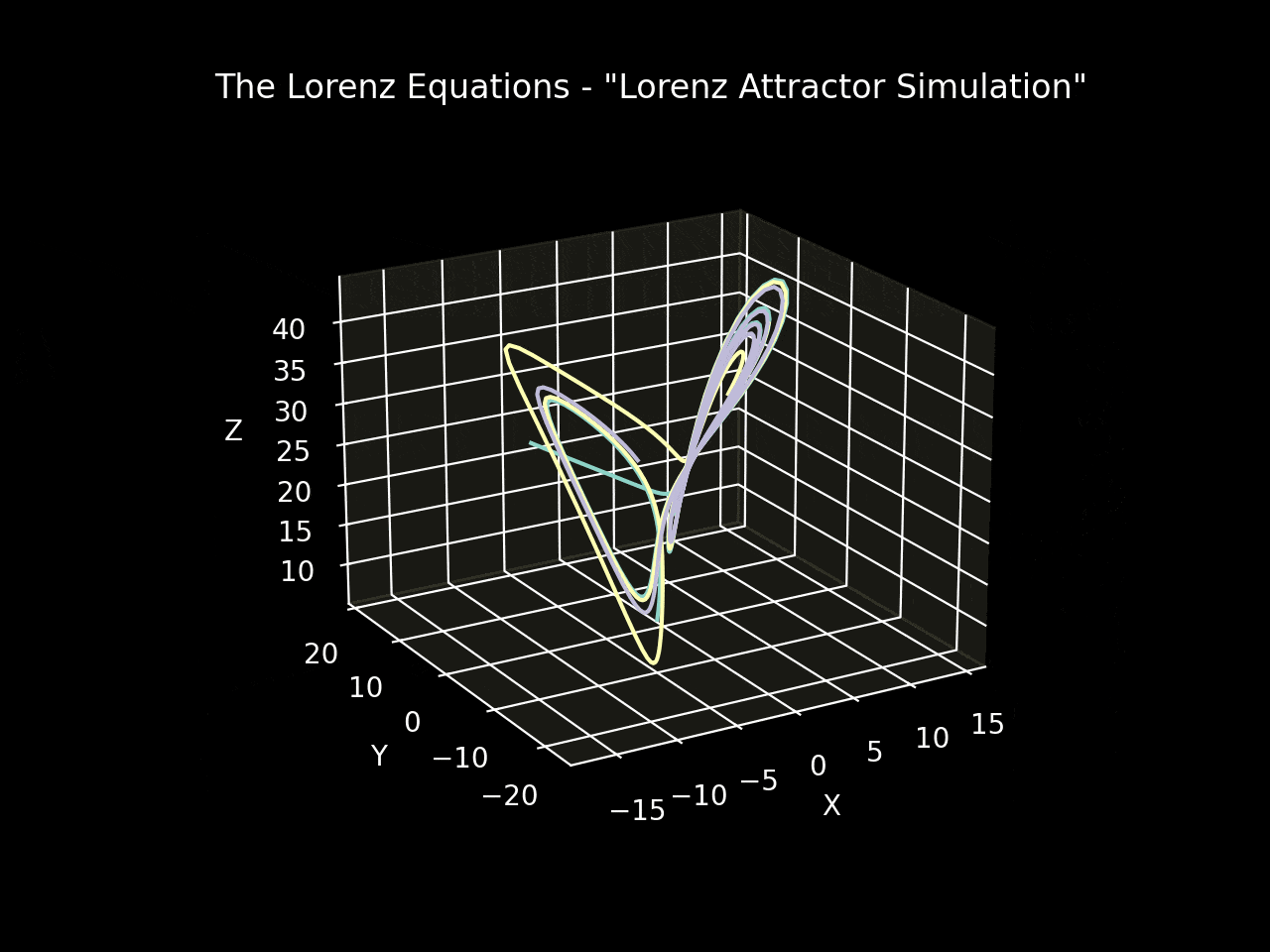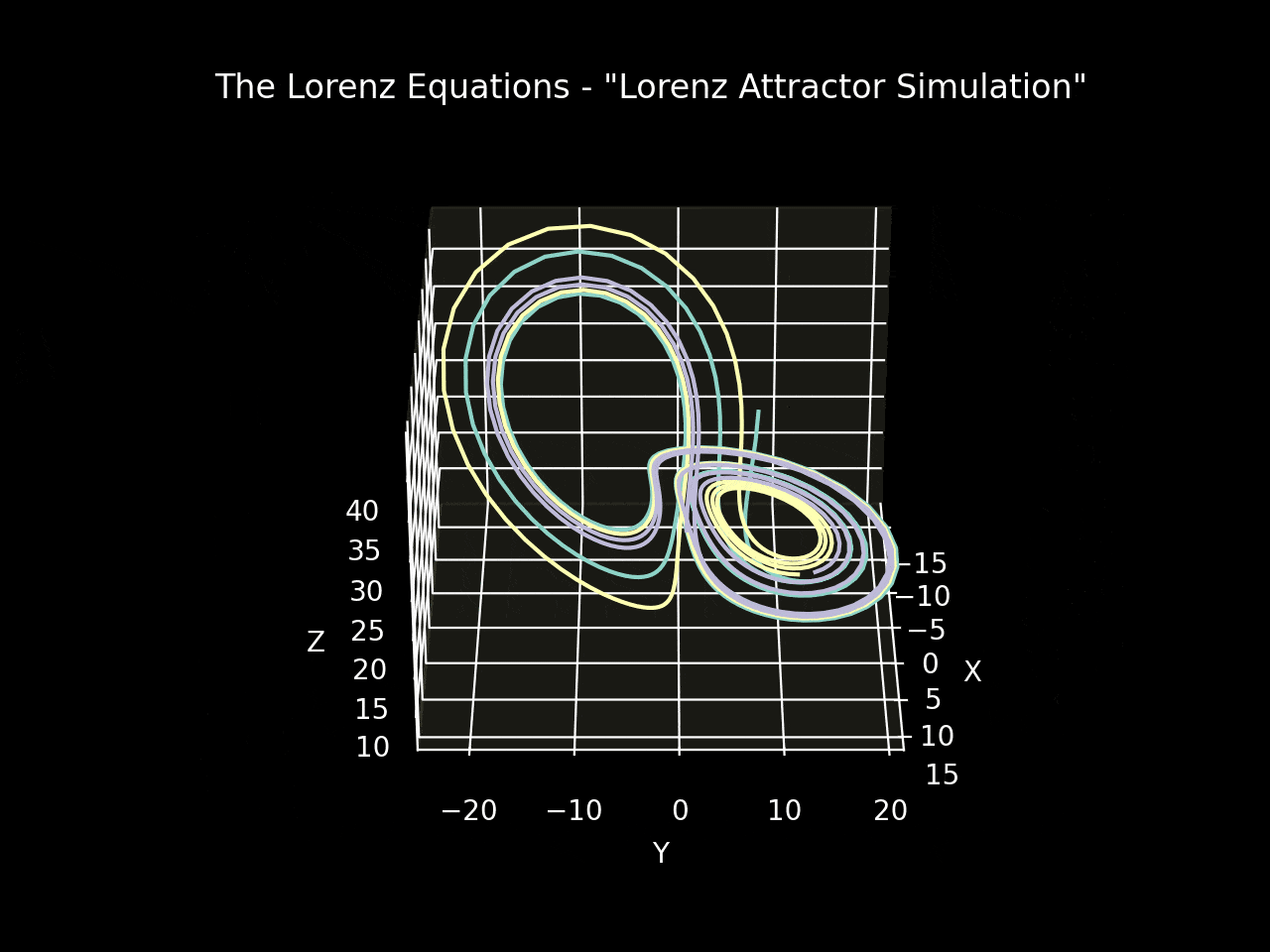
Conclusion
Experimenting with variations in the initial conditions and the coefficients σ, β, and ρ can lead to drastically different system behaviors. This article has successfully demonstrated how to numerically solve and visualize the Lorenz system of chaotic ordinary differential equations through the implementation of the Runge-Kutta numerical integration method in Python.
For further reading, check out the following resources for additional insights into numerical methods in Python and dynamic systems visualization.