Chapter 1: Introduction to Spacetime and Lagrangians

This article aims to unify the concepts of time and space while discussing the Lagrangian formulation in the context of special relativity. Previously, I have elaborated on the Lagrangian method within classical Newtonian mechanics. The elegance of this approach lies in its generalizability. In the realm of special relativity, time is no longer an isolated variable; it is treated as a coordinate similar to spatial dimensions.

Events are now described using four 'spacetime' coordinates, represented as x = (t, x, y, z). Greek indices are employed to denote these four components, where µ = 0, 1, 2, 3. To utilize the Lagrangian framework, our goal is to create an action that allows us to determine the path of an object. In classical mechanics, the parameter that tracks our position along these paths is time itself.

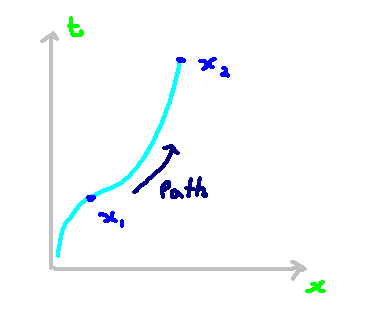
Since our time variable is designated as a coordinate, we must introduce a different parameter to describe paths in spacetime. We will refer to this parameter as ?, and later we will demonstrate a natural choice for it, known as 'proper time.'

We define the metric for this spacetime, specifically the Minkowski metric, as a diagonal matrix represented by ? = diag(?1, +1, +1, +1). Consequently, the distances in Minkowski spacetime can be expressed with the following equation.

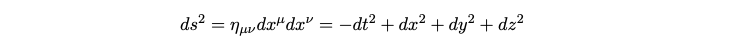
Events are categorized based on their infinitesimal distances. Because our metric lacks positive definiteness, events can possess distances of any sign. The classifications are as follows:

• If ds² < 0, the events are termed timelike.
• If ds² = 0, they are referred to as null.
• If ds² > 0, they are classified as spacelike.

Our action can now be represented in the following manner, utilizing the alternate parameter ? for our path parametrization.

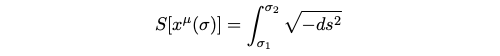
Next, we can express the integrand with the parameter sigma to yield:

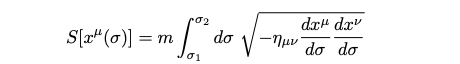
Section 1.1: Symmetries in the Lagrangian

What symmetries exist within the Lagrangian framework? In this context, our Lagrangian L represents the integral term. Before delving into the implications of this equation, there are two significant symmetries worth noting. One of them is invariance under Lorentz transformations. This implies that when we apply a Lorentz transformation x ? ? x, it can be verified that the Lagrangian remains unchanged.

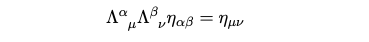
Additionally, this action demonstrates invariance under the reparametrization of the curve via a new function ?’= ?’(?). Utilizing the chain rule, we can reparametrize the action as follows:

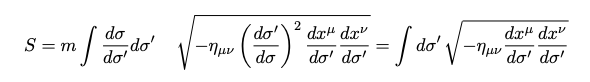
In this scenario, we are simply applying the chain rule while isolating the d?’ / d? term. This results in the same formulation as before, confirming the existence of reparametrization invariance.

Chapter 2: Conclusion

In summary, the Lagrangian approach provides a robust framework for understanding the intricacies of special relativity, particularly through the lens of symmetries and spacetime coordinates.