Chapter 1: Introduction to Number Theory Problems

In the realm of mathematics, particularly number theory, the study of prime numbers captivates many, despite the limited understanding we have about them. This allure is what makes prime-related problems—whether straightforward or complex—so compelling. In this article, we will examine a problem sourced from the Indian National Mathematical Olympiad that combines primes and squares. Before delving into the solution, feel free to tackle the problem yourself!

Let’s first consider the scenario where the prime number is 2. In this case, we would arrive at:

(2–1)/2 = 1/2.

This result is evidently not a square. Since 2 is the sole even prime, we can now proceed under the assumption that p is an odd prime.

We can express p as 2k + 1, leading us to:

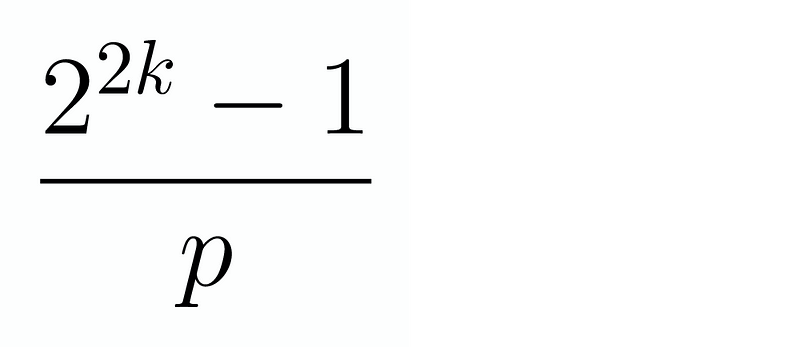
Our goal is to identify values that yield a square, which encourages us to equate this expression to x² for some integer x. Following this thought process, we arrive at:

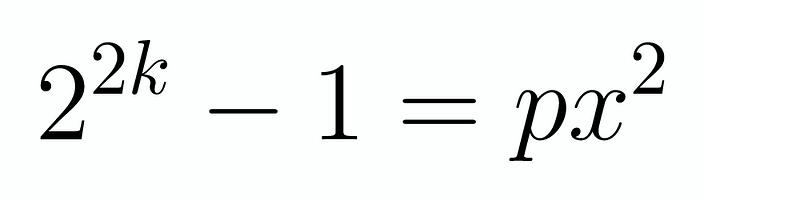
Let’s recall the formula for the difference of two squares, stated as a² – b² = (a-b)(a+b). This aligns perfectly with the left-hand side, allowing us to express it as follows:

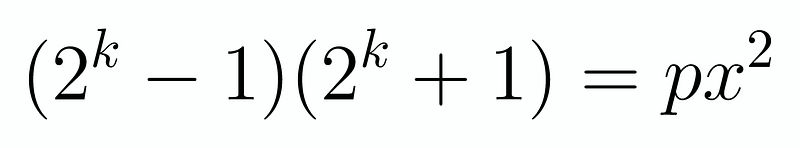
It's important to note that 2^k – 1 and 2^k + 1 share no common factors other than 1. This observation can be confirmed by acknowledging that both terms are odd, thus eliminating 2 as a factor. If we assume some factor d divides both, then d must also divide their difference, which is 2. The only positive integer, apart from 2, that divides 2 is 1.

Consequently, we can equate the factors on both sides individually. Hence, the factors of the left-hand side must correspond to either p or x² separately. This leads us to two possibilities:

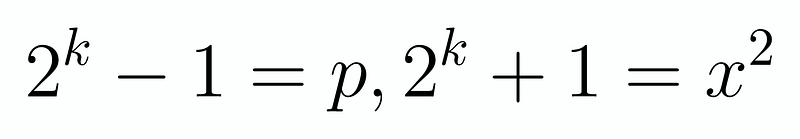
This implies that x² – 1 = 2^k, which subsequently gives us (x-1)(x+1) = 2^k. The only viable solution here is x = 3; otherwise, any number apart from 2 would divide 2^k, resulting in k = 3 and p = 7. Verifying this, we find that p = 7 indeed satisfies the conditions.

Alternatively, we could also have:

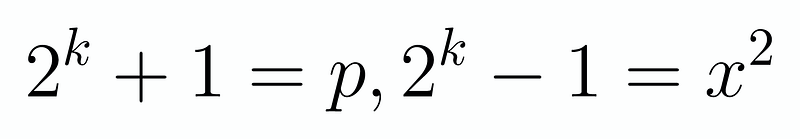
This leads us to the equation (x-1)(x+1) = 2^k - 2. From this, we can derive:

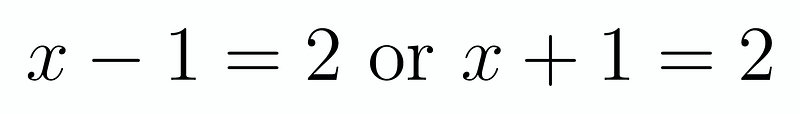
We find that only x = 1 satisfies this case with k = 1, resulting in p = 3. Therefore, our two solutions are:

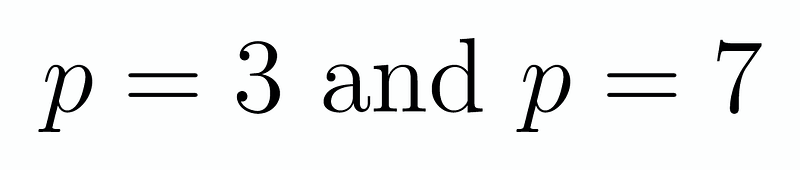
If you found this problem intriguing or enjoyed reading this article, please consider supporting me here. Your contributions are greatly appreciated!

Chapter 2: Video Insights on Number Theory

Explore the fascinating world of number theory through this insightful lecture on sums of squares and Gaussian integers.

Watch as a classic number theory problem is tackled, showcasing the beauty and complexity of primes and squares.