Can You Actually Solve This Third-Grade Math Challenge?
Written on
Understanding the Third-Grade Math Puzzle
Recently, I encountered a math puzzle intended for third-graders that left me pondering. My initial reaction was that perhaps I was not very good at math, or that this puzzle was too complicated for someone in third grade. To make the exercise enjoyable, I chose to think of it as a challenge for anyone, not just kids, and continued to work on it. Eventually, I found a plausible solution. In this write-up, I will detail my thought process in arriving at that answer.
As you follow along, I will provide a ‘spoiler alert’ at a point where you might want to attempt solving the puzzle independently.
The Quest for Patterns in Input-Output Puzzles
When we encounter input-output puzzles, our natural instinct is to search for a pattern that connects the inputs to their respective outputs. We often strive to express this pattern in the form of a mathematical rule or equation. However, in this instance, identifying such a pattern proved to be more challenging.
To help clarify things, I typically create a visual representation of the input-output data. Below is the plot I generated:
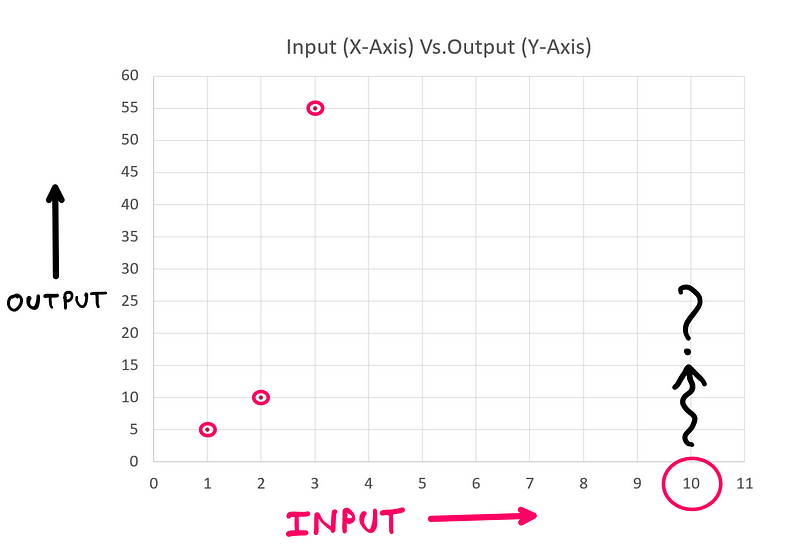
With this graph in hand, it became evident why I initially perceived the puzzle as too advanced for a third-grader. This insight could be the key to solving it.
Before we delve deeper into the solution, it's worth noting that there are countless potential solutions if we consider discrete mappings for each input-output pair. Instead, I encourage you to think about the ‘continuity’ among the various combinations. Using the visual plot as your guide, how would you approach this?
Spoiler Alert: From here on, I will explicitly discuss the solution. If you want to try solving the puzzle independently, you may wish to pause your reading and return later to compare your methods with mine.
Finding the Solution to the Third-Grade Puzzle
Initially, we struggled to discern any patterns from the input-output table. This difficulty arises because humans often think in linear terms. Had the relationship been straightforward, we would have recognized it immediately.
After plotting the data visually, it became clear that the relationship is not linear. The three data points do not align along a straight line, suggesting the existence of a polynomial solution.
The Polynomial Equation Framework
The general form of a polynomial equation is expressed as:
y = ax² + bx + c
where a, b, and c are constants. By substituting the known input and output values into this equation, we derive the following system:
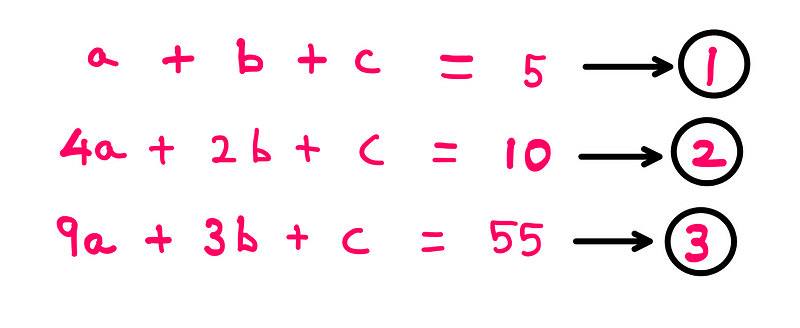
Thus, we have three equations with three unknowns, which can be solved using algebraic methods.
Solving the System of Equations
By subtracting the first equation from the second, we eliminate ‘c’ and derive the fourth equation. Likewise, subtracting the second from the third gives us the fifth equation, which can be compared to the fourth.
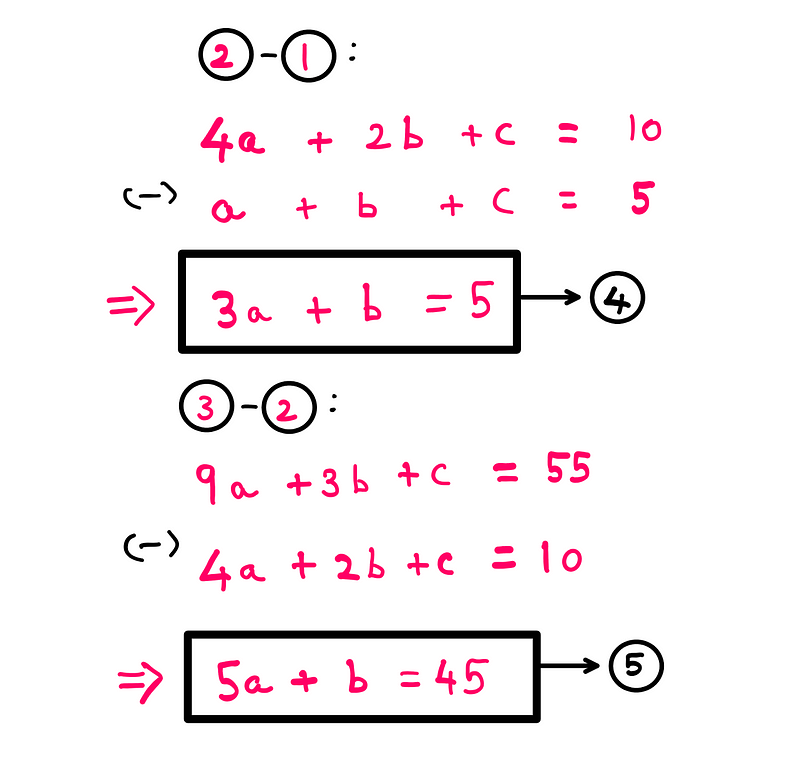
Now, we can subtract the fourth equation from the fifth to find the value of ‘a’:
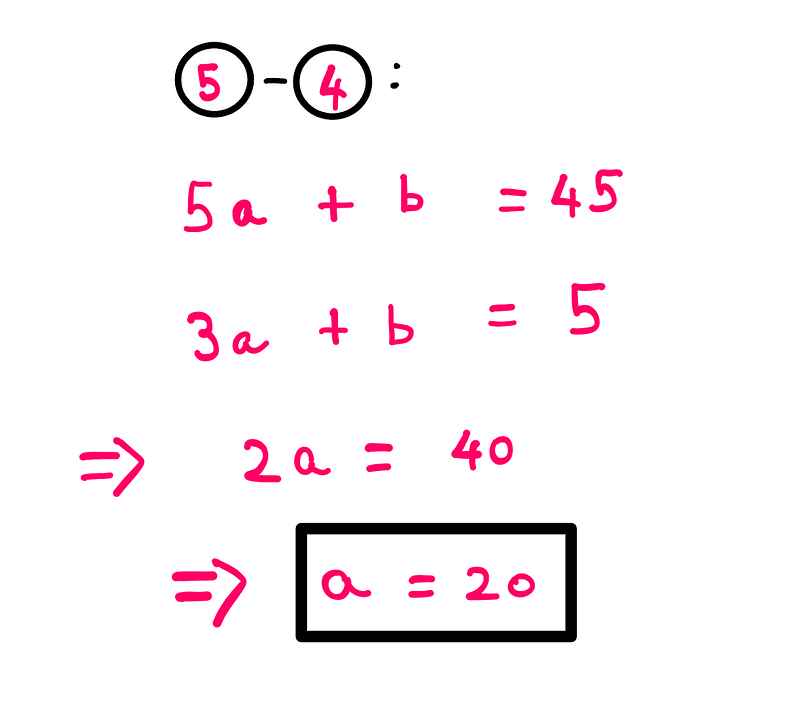
Once we have ‘a’, we can substitute it back into the fourth equation to discover ‘b’:
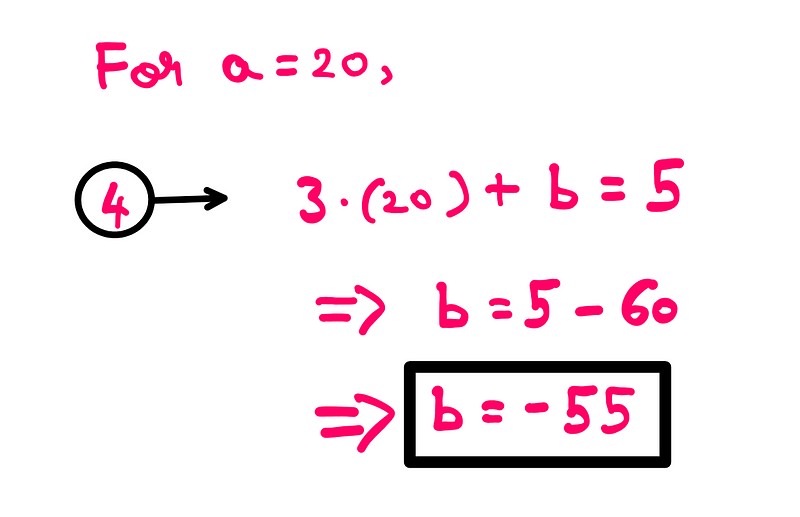
Finally, substituting both ‘a’ and ‘b’ into the first equation yields the value of ‘c’:
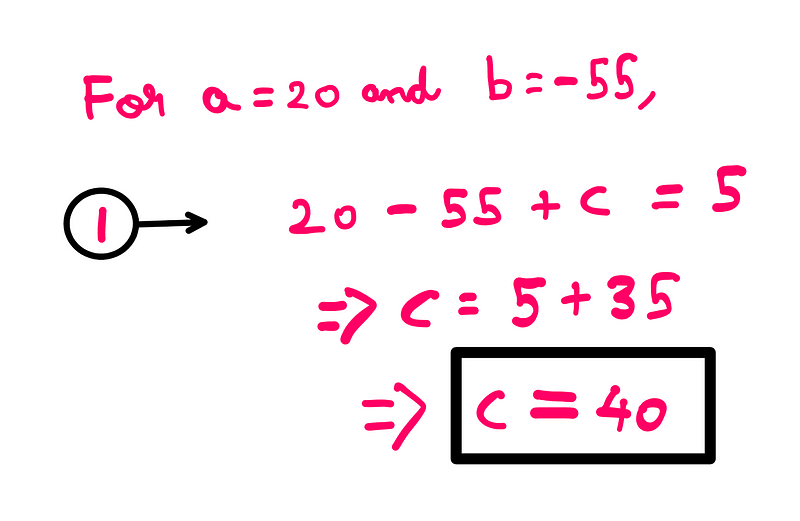
The Ultimate Solution to the Third-Grade Challenge
To find the final answer to our third-grade puzzle, we substitute the values of ‘a’, ‘b’, and ‘c’ back into the original polynomial equation for ‘x = 10’ to find ‘y’:
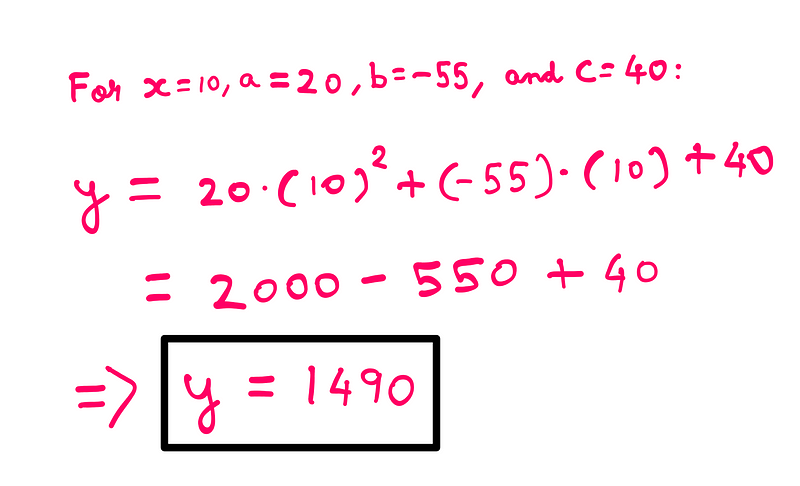
And there you have it—the solution to the puzzle.
Final Thoughts
It is evident that this puzzle exceeds the typical third-grade level. My assumption (and that of others) is that a typographical error likely occurred in the original problem statement. If we were to change the output for the input ‘3’ to ‘15’, it would create a linear relationship, making the puzzle much more accessible for a third-grader.
In any case, I utilized the original puzzle as a springboard for some mathematical exploration and created hand-drawn illustrations along the way. I trust you found the experience as enjoyable as I did!
An Elegant Alternative Solution
William Crendal suggested that alternative, non-polynomial solutions may be more intuitive for children. For instance, one could express the input as a combination, such as 3 = 2x1 + 1, and derive outputs based on this logic, leading to various solutions for ‘10’.
Source and Credit: r/HomeworkHelp and Presh Talwalkar.
If you’d like to support my work as an author, please consider clapping, following, and subscribing.
For further reading, you might find interest in topics like "How To Calculate The Day Of The Week For Any Date?" and "How Easy Is It Really To Predict The Future?"
This video titled "Can you solve this elementary math puzzle? | Puzzle 4" presents a fun and engaging challenge that may help sharpen your problem-solving skills.
In this video, "Can you solve this puzzle?| Math Puzzle for Kids 3," viewers are encouraged to tackle math puzzles designed specifically for younger audiences.