Understanding Time and Space Complexity in Recursive Algorithms
Written on
Chapter 1: Introduction to Complexity Analysis
In this article, we will explore the analysis of time and space complexity in recursive algorithms by investigating two well-known examples: the Fibonacci sequence and binary search. Gaining insights from these examples will enhance your understanding of recursive algorithms.
Performance of Recursive Fibonacci Calculation
We begin by examining a recursive method to compute the Fibonacci sequence:
def fibonacci_recursive(n):
if n <= 0:
return 0elif n == 1:
return 1else:
return fibonacci_recursive(n - 1) + fibonacci_recursive(n - 2)
Time Complexity Analysis
While recursive algorithms are often succinct and may use minimal storage from an algorithmic perspective, this does not imply reduced memory consumption during execution. Let’s analyze the time complexity of the Fibonacci algorithm provided above.
The time complexity of a recursive function fundamentally depends on the total number of recursive calls multiplied by the complexity of each call. In this instance, each recursive invocation is an O(1) operation. We can visualize the recursive process for an input of n = 5 using a recursive tree:
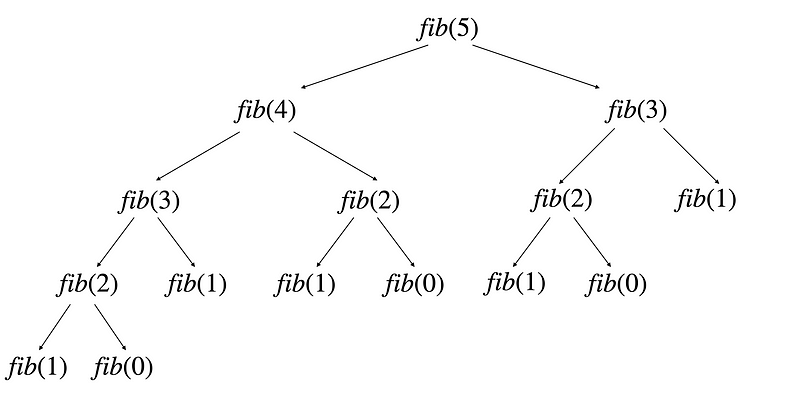
#### Example of Fibonacci Calculation for n = 5
The recursive tree illustrates that for n = 5, multiple recursive calls are made for smaller values of n. The exponential growth in calls becomes evident as n increases because each Fibonacci computation generates two additional recursive calls. The number of nodes in this recursive tree for n can be approximated as $2^n$. Consequently, the time complexity of the recursive Fibonacci algorithm is O($2^n$).
It is crucial to recognize that this approach exhibits exponential time complexity, making it impractical for large values of n. For better efficiency, consider using techniques such as memoization or iterative methods for larger inputs.
If we modify the code to:
def fibonacci(first, second, n):
if n <= 0:
return 0if n < 3:
return 1elif n == 3:
return first + secondelse:
return fibonacci(second, first + second, n - 1)
This variant employs tail recursion, wherein the recursive call is the final operation in each recursion branch. Consequently, the function executes exactly “n” recursive calls, where “n” indicates the Fibonacci number index.
Breakdown of Time Complexity Analysis
- For n <= 0, the function executes in constant time, O(1).
- For n < 3, it also returns in constant time, O(1).
- For n == 3, a single recursive call is made, resulting in O(1) time.
- For n > 3, the function calls itself with n - 1, repeating "n" times, culminating in O(n) time complexity.
In summary, the time complexity of this modified code is O(n), which is considerably more efficient than the exponential time complexity of the earlier method.
Space Complexity Analysis
To understand space complexity, consider that it equals the space used by each recursive call multiplied by the recursion depth. It is essential to gauge recursion depth since each call's memory is added to the call stack (a structure for managing memory, akin to the stack concept in algorithms). After each call concludes, its data is removed from the stack, making the maximum stack length equal to recursion depth.
Let’s assess the space complexity of the first code snippet. Each call requires a constant amount of space, O(1), which does not vary with n. Thus, the space complexity for each call is O(1).
Now, let’s evaluate the recursion depth, as illustrated:
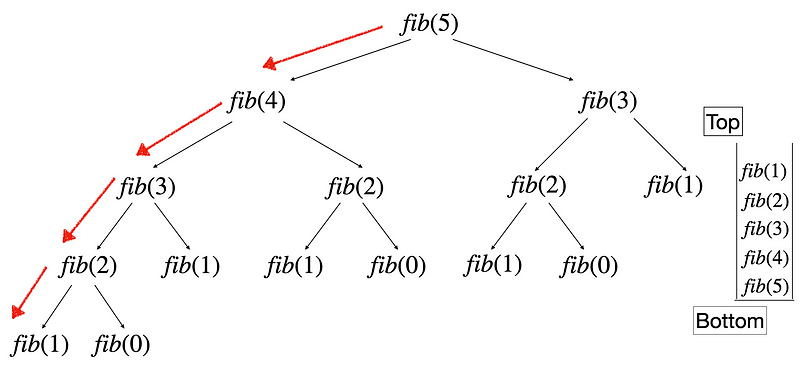
When calculating the nth Fibonacci number through recursion, the depth of the call stack reaches n. Given that each call has a space complexity of O(1) and the call stack depth is n, the overall space complexity is O(n).
A similar analysis applies to the second method.
Summary
In this article, we provided a comprehensive analysis of space complexity in recursive implementations for Fibonacci calculations. We compared two recursive methods and noted a significant disparity in their time complexities. Our experiments confirmed that O(2^n) time complexity is extremely demanding. We hope this insight proves beneficial, and we encourage you to keep time and space complexity in mind during software development!
The first video explains the time and space complexity analysis of recursive programs, specifically using the factorial example.
The second video covers space complexity related to recursive algorithms, providing further insights into this critical topic.